At its most basic, here is what science is all about. Observations are made of how some aspect of the universe works. Measurements are made to attach numbers to the observed events and a theory is invented that explains the numbers. What the theory allows us to do is to calculate the results of experiments which have not been done yet. The theory is tested by having its predictions compared to yet another observation. If there is agreement between the predictions of the theory and experimental results over a long time with many experiments and experimenters, eventually we accept that theory as one of the "laws of nature" which govern the working of the universe. In the course of the verification, or even later after a theory has achieved "law" status, if a verifiable experiment comes up with a discrepancy between the theory's prediction and experimental observation, we go back and scrap the theory or modify it to cover the new observations. This cycle of theory and test boils down to the pursuit of truth. The pursuit of objective truth, truth that is verifiable by anyone willing to expend the effort, has been and is the most productive activity in which humankind has ever engaged.

For us to participate in scientific discovery, we need to be solidly grounded in the basics. That is the purpose of this course on mechanics. There are a few fundamental concepts we need to nail down before we begin toying with some of the laws of nature that were established by others. And, we must really understand those laws before we can begin to think about extending the scientific process I described in the previous paragraph.

First let's think about physical quantities . These are the building blocks in terms of which the laws of nature are expressed. Among these are length, mass and time and a lot of others derivable from these. Examples of quantities that may be derived from distance, mass and time are force, velocity, momentum, energy and acceleration.

Those physical quantities which are distinctly associated with an object , like mass for example are called properties of the object. As we deal with these quantities I will try to always be clear on exactly which I am working with. There is nothing magic by the way about the choice of length, mass and time as the fundamental quantities. We could have begun with others and derived these.

Now if we are to determine useful things about objects in terms of the physical quantities, we must agree on the units of measure of these quantities. Units of measure allow us to answer the "how much" questions. How much length? How much mass? How much time? I will mainly to stick to the International System (SI) which has become the most commonly accepted for scientific work. In this system of units the standards are: length - meter, mass - kilogram and time - second. If you insist on using a furlong, stone weight, fortnight system you will probably end up spending a lot of time doing unit conversions.

Are there any questions?

Mechanics is the study of objects in motion so we are going to need a way to describe both objects and motion. At this stage of the story we are going to limit ourselves to objects that may be regarded as particles. A particle is a bit of matter whose size is small enough relative to our observations that its dimensions may be neglected. For example the Earth might be considered a particle if we were studying its orbit around the Sun, but not if we want to know anything about its rotation about its axis. The nucleus of an atom might be a particle in an experiment on elastic scattering , but not in considering nuclear fission.

Under the restriction that our objects are going to be particles, the only property related to mechanics an object can have is mass. This means that to describe an object only requires that its mass be specified. Any other property you can imagine, let's say density for example, requires that the object have some size.

Now let's examine what we mean when we say something is in motion. We are all familiar with motion. Birds move. Cars move. We see examples of motion all the time. All we need to do is to quantify this everyday experience a bit to apply it to mechanics. Motion always implies the passage of time. Let's define two specific times called early and late. If an object is found at a different position at time=late than where it was at time=early then we say movement took place. If there is still a difference in position when time late is as close to time early as we can imagine, then we say the object is in motion.

The word "dimension" showed up recently in the sense of the extent of an object. The other sense of that word, dimension, has to do with the nature of the space being considered. For our purposes, neglecting Einsteinian relativity, we live in a three dimensional space. The surface of a sheet of paper or a computer screen might represent a space of two dimensions. A single line, like the number line , represents a space of one dimension.

The words "infinite" and "infinitesimal" also need a bit of explanation. I would like to have infinite mean big enough so that bigger makes no practical difference. An infinite distance, under this definition, might be 1 centimeter if we are discussing the gravitational attraction between two molecules. Let us agree that infinitesimal is small enough that smaller doesn't matter. Like the radius of the Earth in considering planetary orbits.

Another fundamental concept in mechanics is that of an observer and the observer's frame of reference. Frequently we give no thought to the observer or the reference frame in everyday life because we ourselves are doing the observing and our frame of reference is a system of measure relative to the location of our eyes. For example we judge location by how far left, how far up and how far away. We determine motion by noticing a change in location. In this course I will be asking you to imagine experiments in which the observer's reference frame may be other than your own.

As I mentioned, intuitively we detect motion as a change in position over time. In mechanics it is the same but we need more than "eyeball" precision in determining position. We will quantify the position of particles by measuring from a fixed point in our reference frame to the particle. The fixed point from which measurements are made is called the "origin" of the reference frame. There are two convenient ways to measure the position of a particle. One is to measure along the dimensions of the space in which our reference frame is constructed. The other is to measure the distance and direction from the origin to the particle.

Suppose we wish to measure the position of a particle which could only move in a straight line. We would choose a one dimensional space in which to study the motion since the other possible dimensions do not add any intelligence. The reference frame would then be a real number line called an axis and the position would be just how many length units the particle was from the origin. In this one dimensional model, the two ways of measuring position are identical. The particle must lie exactly on the one axis of the reference frame so the measure along the dimension of the reference frame is the distance from the origin to the particle. The Real Number Line display seen previously is an example of a one dimensional reference frame.

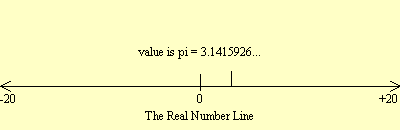
Now consider a case where a particle is constrained to stay in a plane, that is on a flat surface. Here we would choose a two dimensional space in which to study the motion. We choose the reference frame to be two number lines (axes), perpendicular to each other with zero as their common point. Making the lines perpendicular is a trick to simplify the mathematics but any two non-parallel lines could serve. Any set of lines that could serve as axes for a reference frame is said to "span" the space in which the reference frame is constructed. Traditionally the horizontal axis is labeled the x axis and the vertical the y axis.

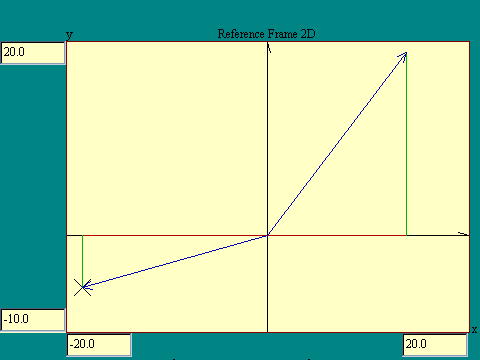
Working in two dimensions, we now have distinct ways of locating a particle. One is to measure its position along one of the axes, then measure its position parallel to the second axis. That pair of numbers, called the coordinates of the particle uniquely establish its position. One way of designating the coordinates is to place the two numbers in parentheses like (a,b). This notation is called an ordered pair. The x coordinate (a) is always first then, separated by a comma, the y coordinate (b).

The other way of locating a particle is to measure the distance from the origin to the particle and measure the angle of that line from the horizontal axis so that we have a magnitude and direction. Run the Reference Frame 2D display to see these concepts in action.

Finally think about a particle that is free to move in three dimensions. To span a three dimensional space we need three axes for our reference frame. Again we will make them all share a common zero and be mutually perpendicular. Sometimes you may see the word "orthogonal" to describe lines that are all perpendicular to each other. Again we could locate a particle by giving its coordinates (a,b,c) or by giving the distance and direction from the origin of the reference frame. Note that the direction in three dimensions now requires two angles, a latitude and longitude for example. As a general principle it will require as many numbers as there are dimensions in our space to specify the location of a particle. The number of numbers required to specify the position of any object, not just a particle is called the "degrees of freedom" of that object.

Up to two dimensions, the representation of the reference frame on the monitor screen posed no problems. Once we add the third dimension, the two dimensional nature of the screen gets in the way. Some imagination will be required to see this flat display as three-dimensional. Picture the situation like this. Begin with the x and y axis as described in the two dimensional case. Now suppose that instead of the axes lying on the surface of the screen, the screen is a window through which you look to see the reference frame axes somewhere behind the screen. Also imagine that there is another invisible horizontal axis parallel to the screen through the center of the volume of space outlined in the display, about which we may rotate the image. We will call this the pitch axis.

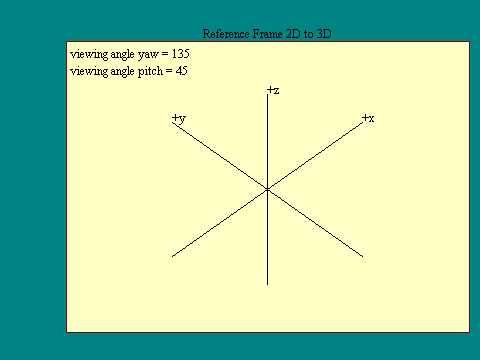
Next imagine that I draw a third reference frame axis, with its positive end sticking straight toward the screen. Call that axis the z-axis. Since the z-axis is sticking straight toward you, you can not see it until we rotate the frame about the pitch axis. In fact we will rotate it around both the pitch axis and the newly created z-axis in the next display. The angle through which an object is rotated about the pitch axis is called the pitch angle, about the z-axis, the yaw angle.

The choice of which axis is x, which is y and which is z is sometimes a bone of contention among different branches of science and always a point of confusion if not spelled out. What we will use is called a right-handed reference frame. That means if you hold the thumb, fore finger and middle finger of your right hand more or less at right angles to each other, your thumb will point along the positive x axis, your fore finger will point along the positive y axis and your middle finger will point along the positive z-axis. Whatever orientation you hold your hand in, the relationships among the axes will be the same.

Run the Reference Frame 2D to 3D display for an illustration of this kind of reference frame.

We have been observing the reference frames we have talked about from somewhere outside the frame itself. If the reference frame was really a solid object suspended in space, we could walk around it and presumably view it from above or below. We may find it convenient to look at frames that way or we may wish to view objects as if we were in the frame ourselves. Remember we created the idea of a reference frame so that we could determine where things were located and many times we want to know where they are relative to us, the observer. If we do choose to look at a reference frame from the outside, we may want to re-orient the frame so as to see objects in the frame from various perspectives.

Now for one other problem which comes up when looking at three dimensional reference frames. In one and two dimensions the screen cursor served to point out locations in the reference frame. In three dimensions only two of the axes can lie in the plane of the screen where the cursor is. And depending on the orientation of the frame in the monitor, none of the axes must lie in that plane. So the cursor is unavailable for us to use in marking positions. To identify a point in a three dimensional frame we will have to specify the distance along each of the axes to the point. Run the Reference Frame 3D display to see how this will work.

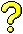
Are there any questions?

We have spent a lot of time describing how to locate objects in spaces of 1, 2 or 3 dimensions. Much of our work will be done using a two dimensional representation, even if we are considering a single dimension of space. That will allow us to plot position as a function of time. In fact we have been a little fast and loose with the idea of locating an object. Not only must we specify x, y and z, but also when. We will speak more about this idea later.