Let's begin this journey together more or less at the beginning with a quick review of numbers and arithmetic. Certain numbers are called "real", which seems to mean that there are others, possibly unreal. Real numbers may be thought of as lying along a straight line with zero in the middle and extending as far as imaginable to the right for positive numbers and as far as imaginable to the left for negative numbers. Included are whole numbers (integers), fractions (rational numbers) and decimals not expressible as fractions (irrational numbers).

The image at the right illustrates a short segment of the real number line, between -20 and +20. The indicated example here is an irrational number. Click on the link for the Real Number Line interactive display from which this example was taken.

Real numbers may be added, subtracted, multiplied and divided in the ordinary way. In this program we will use the following symbols for mathematical operations. For addition +, for subtraction - , for multiplication *, and for division /. Raising numbers to powers, sometimes called exponentiation, we place the exponent above the number and to the right, like 3⁴, or we use the ^ symbol like 3^4. Both mean 3 multiplied by itself 4 times. Numbers may be raised to non-integer powers like 2.7^0.5. This is the square root of 2.7. Applying any combination of addition, subtraction, multiplication and division to real numbers results in another real number. Raising real numbers to powers also gives a real result in many cases. We will cover the interesting exception later.

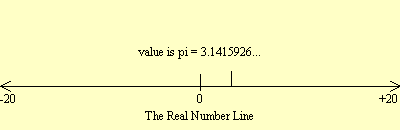
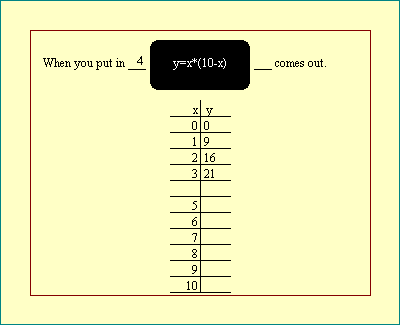
Sometimes mathematicians like to make up rules that produce one number from another, like take a real number and divide it by two to get another real number. Or take a number, multiply it by itself and add a second number to it to get another number. The possibilities are nearly endless. In this program we will deal with some of these rules for combining numbers which in themselves are fairly simple but which under the conditions we will explore, produce wonderfully complicated results. Don't worry, the complications are wonderful but not fearful.

This making up of rules is more than a means of filling the idle hours. It turns out that many physical phenomena may be described by rules like this. Rules of the sort we cover here are called "functions". The number produced is said to be a function of the number "taken" at the beginning. In particular these are called a single valued functions. Each number in, gives one number out. The "taken" number is called the "independent variable" the produced number the "dependent variable". We talk about a function as "returning" the dependent variable.

Frequently the independent variable is called "x" and the dependent variable called "y". We will refer to x and y in that in the rest of this discussion. Some functions have restrictions on the allowed values of x. The set of all values of x which are allowed for the function is called the "domain" of the function. The set of all values of y which the function returns is called the "range" of the function. The word "set" as we will use it just means a collection of related objects or numbers. The mathematical definition is very close to ordinary usage.

In addition to the arithmetic operations of addition, subtraction, multiplication, division and exponentiation; there are other defined functions that operate on real numbers. In particular there are two, which we will use in our examples later. The sine function, symbolized as

Sometimes it is useful to look at the way that y depends on x by plotting the relationship on a graph. We plot the x value along the horizontal direction, called the "x-axis". For each value of x the corresponding value of y is plotted over x in the vertical direction, called the "y-axis". The series of y locations traces out a curve which represents the function. Recognize that any graph represents only a sampling of points covered by the function. It is an accurate representation of the function only if the function has no bizarre behavior between sample points.

On the Graphing display we will demonstrate how a function may be represented by a graph.

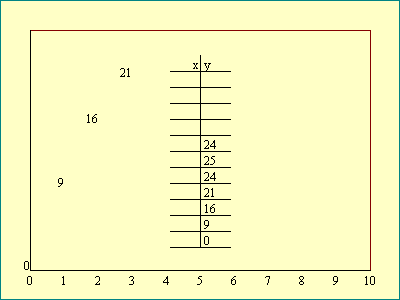
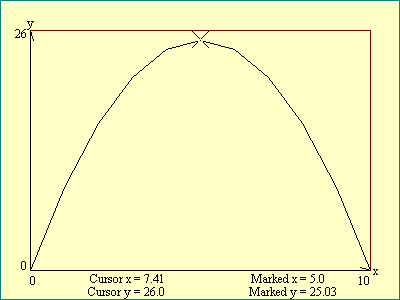
For purposes of introducing the graphing concept, marking the y values with the actual number was OK, but as a practical matter we will not want our graphing illustrations peppered with numbers. We could replace the y numbers with some more convenient marker and move the values to the y-axis as we did with the x values. If this were a paper graph that is what we would do. Then to determine the x and y values called "coordinates" of any point on our graph we would have to estimate the values from the axis scale.

Fortunately we are going to work with computer graphs rather than paper ones. On the computer screen we will take advantage of the cursor provided to us by our operating system. The coordinates of the point on our graph pointed to by the cursor can be displayed and updated as the cursor is moved. The x and y values are displayed in the bottom margin.

Run the Cursor Action display to see the rudimentary graph produced in the Graphing display replaced with a better version.

We draw graphs by selecting a few points along the x-axis, calculate the corresponding y values, plot those points and then connect the dots to fill in all the other uncalculated points representing the function. What we assume in doing this is that the function is fairly smooth and behaves on a small scale pretty much the same way it does on the larger scale covered by the points that were calculated. Sometimes we refer to functions for which this is true as "well behaved". Functions which represent actual physical systems tend to be well behaved.

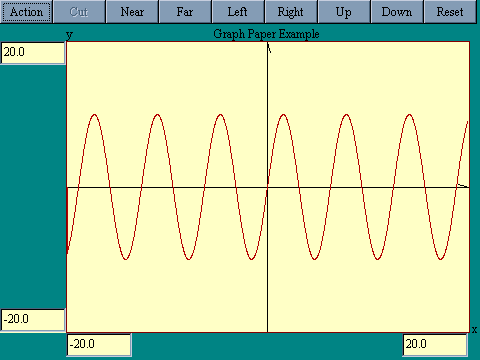
We are going to need some graph paper on which to draw graphs and other forms of program output. It will sometimes be convenient for you to be able to control the boundaries of the region displayed on the drawing area. Also the program output may sometimes be animated and you will need some way to start and stop the action. We will use a sort of generic graphing display with controls on it to allow the functions we described. The image at the right is a screen shot of the graph paper applet. In cases where there is no need to change the limits or start and stop the action, the controls will be disabled. Run the Graph Paper display. An explanation of the controls is attached.

This concludes this bit of background material. Use your browser's "Back" button to return from whence you came.