In our previous discussion of one-dimensional motion we used a model in which the acceleration was itself a varying function of time. By introducing yet another simplification, we can get at several interesting examples of motion without getting bogged down in complicated mathematics. Consider the case of acceleration that is constant over time. This case is actually what we see when objects are accelerated by gravity near the surface of a planet such that the distance the object covers in its travels is small compared to the distance to the center of the planet. You know, tossed eggs, thrown rocks, cannon balls... that sort of thing.

With acceleration being a constant, the average value which is given by = (v_f - v_i) / (t_f - t_i), which is the same as the instantaneous value. The subscript _i refers to an initial condition and the subscript _f refers to a later condition. The initial velocity v_i is that measured at time t_i and the final velocity v_f is that measured at time t_f.

To simplify our handling of time, recognize that we are always going to be dealing with changes in time, like t_f - t_i. Now if I add any arbitrary constant to both t_i and t_f, the difference will be unchanged. For example let us suppose there have been 5e17 seconds since the beginning of time. (By the way if you are not familiar with the notation, 5e17 means 5 times 10 raised to the seventeenth power or 500,000,000,000,000,000.) Then t_i might be 5e17 seconds and t_f might be 5e17 seconds+1. The difference is 1 second. If I add -5e17 to both t_i and t_f then t_i = 0 and t_f = 1. The difference is still 1 second. So we are free to let t_i = 0 as long as we let t_f be measured in seconds beyond t_i. Now since t_i may be arbitrarily set to zero, there is no reason to continue to label the final time with an _f. Let's just call it t, so = (v_f - v_i) / (t - 0).

To further clean up the notation, since the initial time is always to be taken as zero, let's call the initial velocity associated with it v₀. Also what we called v_f was just the velocity measured at time t_f, which we now identify as just plain t. So we can drop subscript _f from velocity measured at time t, calling it just plain v.

Now here is one of those ideas that has always struck me as a little bit sneaky. We have been working so far with two discrete times, initial and final. We got rid of the initial time by agreeing to let it always be zero. Then logically we could take the "final" designation off the other value of time. Now the quantity t is not any specific value. It may be taken to be any number of seconds that suits us. In other words t may be considered a variable.

The only restriction on v is that it is the velocity corresponding to time t. That makes v also a variable, dependent on the independent variable t. So we have come to a relationship between t and v similar to that we defined for x and y in our discussion of functions .

To symbolize the functional relationship we write v = f(t), which is said, "v equals f of t", or "v is a function of t". The symbol f stands for any particular function we choose. In terms of our earlier talk about functions we could have said y = f(x) This way of identifying that two variables have a dependency relationship is called "functional notation". It allows us to know that v is a function of t without knowing the details of the function.

Getting back to our expression for acceleration, remember that the instantaneous acceleration is the same as the average acceleration so that a = (v - v₀) / t. Since v = f(t), we can rearrange the acceleration equation, a = (v - v₀) / t to find out what specific f(t) v is. Multiply both sides by t so that a * t = v -v₀. Then add v₀ to both sides so that v = v₀ + a * t. 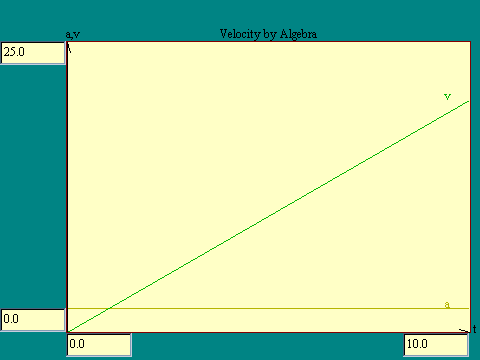This means that the velocity at time t is its initial value plus the change in velocity during time t. To see the relationship between the velocity v and the acceleration a, run the Velocity by Algebra display. In this display the velocity at each time is calculated from the equation we just developed.

There is an alternative, and powerful, way to get the velocity from the acceleration. Back in the introduction to this course, in the last few lines, I introduced the prospect of undoing the work Newton did in replacing millions of trivial calculations with a few complex ones. We are going to go back to the commonsense idea that the amount of stuff present at any time is the amount at a previous time plus and minus any changes. This notion by the way is the foundation of that branch of mathematics called differential equations. Applying this to velocity, the change in velocity between time t and time t+dt is the average acceleration over that interval times the duration of the interval dt, where dt is just the name we call the difference in time. Notice that the symbol dt plays the same role as the Dt we used when talking about finite time differences. The dt symbol is used in instances where the duration of the time interval may become smaller without limit, approaching zero if required. It is a subtle distinction, but then mathematicians are like that - subtle.

The way we will handle getting velocity from acceleration without necessarily knowing the function f in v = f(a), is to slice time up into equal intervals of width dt and add up the changes in velocity over each interval between time zero and time t.

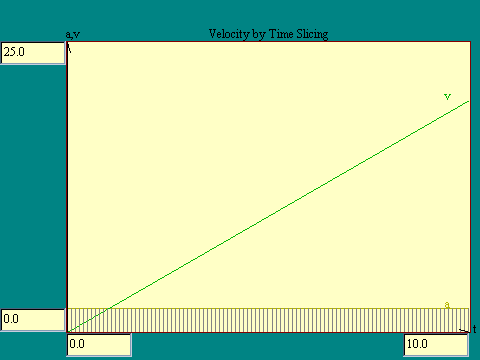
Look at the Velocity by Time Slicing display to see the velocity curve developed in this way. Notice that the change in velocity during any time interval is just the area of that little rectangle of width dt and height a. The value of velocity at any time is just the sum of the area of all those little time slices to the left of that time. In other words velocity at any time is the area under the acceleration curve up to that time. Of course since we are working with constant acceleration, the area of each time slice is exactly equal to dt times the a at any point in the slice.

Next we will work on the displacement of our particle undergoing constant acceleration. Because the acceleration is constant, the average velocity over the interval of time between 0 and t is = (v₀ + v) / 2 using the normal averaging formula. If the rate of change of velocity were not uniform, i.e. acceleration a constant, the average would have to be some sort of weighted average. We could not get it from just the initial and current velocities. If the position of the particle is x₀ at t=0 then the position x at time t is given by x = x₀ + * t . This follows from the definition of an average velocity. But is 1/2*(v₀+v) so x = x₀ + 1/2 * (v₀ + v) * t. Or, if we choose the origin of our reference frame such that x0=0, x = 1/2 * (v₀ + v) * t = 1/2 * v₀ * t + 1/2 * v * t. We may substitute for v in the preceding equation, v = v₀ + a * t, giving the result x = 1/2 * v₀ * t + 1/2 * v₀ * t + 1/2 * a * t². Or x = v₀ * t + 1/2 * a * t².

Now we may add the displacement x to our graph of the parameters of the motion of a particle under constant acceleration. Look at the Displacement by Algebra display to see this.

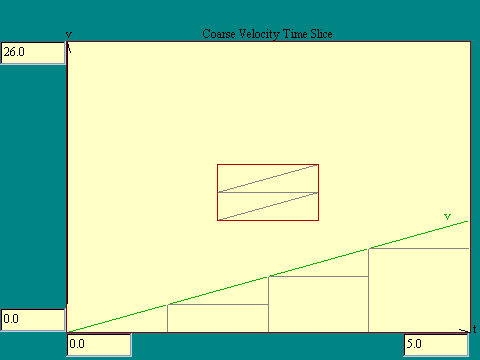
Just to revisit the idea of a parameter being related to its rate of change by the area under the rate of change curve, look at the development of displacement from the area under the velocity curve. In this case we need to pay more attention to how we calculate the area. In calculating the area under the acceleration curve previously there was never a question about what height to use for our time slices. They were the same height everywhere. Since the velocity curve is not flat, each time slice has a low side and a high side. If you use the high side dimension the calculated area of each time slice will be too large. If the low side is used the area will be too small. Look at the next display, Coarse Velocity Time Slice for an illustration.

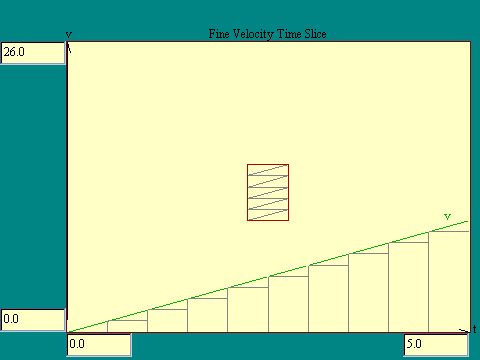
Now suppose we increase the number of time slices as illustrated in the Fine Velocity Time Slice display. The images above and at the right illustrate the total error in area under the velocity curve for two dt values, one large and the other smaller. If you count up the little triangles stacked in the red boxes you will see in each instance that the total error is the same as the area of a single time slice, centered along the t-axis. The altitude at the midpoint of the velocity curve fixes the height of such a time slice. The width of that time slice is just dt. As we make more time slices by reducing dt, the error area must decrease. In fact we can reduce the error between the actual value of v at any t and the total area under the curve up to that t, to less than any arbitrarily small value by choosing dt small enough.

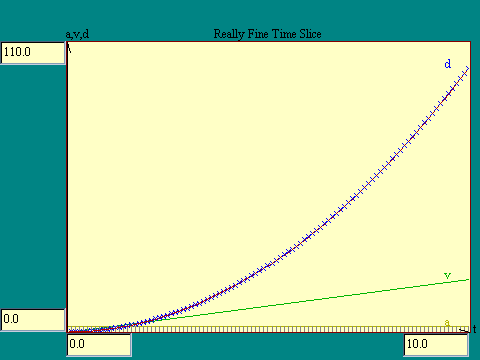Finally take a look at the Really Fine Time Slice display to see how closely the area under the velocity curve fits the displacement curve calculated from the formula we developed. You can see that with 100 time slices, the error is about as small as the screen resolution. The computer could easily handle 1000 or 10,000 time slices, which is fine enough for all practical purposes.

Are there any questions?

Here might be a good place to relax for a few minutes, like these guys, and look back over the trail that brought us to this point. Working in 1 dimension, we defined the idea of the position of a particle as a distance from the origin of a reference frame. Then we defined velocity as the rate of change of position with respect to time. Next we defined acceleration as the rate of change of velocity with respect to time. Armed with those definitions you will be able to determine average values of velocity if you have a plot of position vs. time, and average values of acceleration if you have a plot of velocity vs. time. By taking smaller and smaller dt, you can make the average values as close to the instantaneous values as you like. In the limit as dt approaches zero, the average value approaches the derivative of the function, dx/dt, which is the slope of the curve.

Frequently it is the position as a function of time that is unknown and the acceleration that is known. In the case where the acceleration is constant we derived an expression for the velocity and position as functions of time using the fact that the average acceleration and instantaneous acceleration have the same values. Then we made the case that a general way to get the value, at time=t, of a variable from its rate of change was to calculate the area under the rate of change curve from zero to t. And, that we could calculate that area by summing up the areas of time slices, reaching any required precision by taking small enough dt. This last result is of profound importance.

It was the realization by Isaac Newton that the sum of tiny rectangular slices could be made to approximate the area under any reasonable curve that led to the invention of integral calculus. In principle Newton and his contemporaries could carry out the simple multiplication and summing process for thousands or millions of little rectangles. As a practical matter however life is too short to get very far that way using a quill pen and parchment. So they had to come up with a trick to replace the millions of trivial calculations with a few complex ones. If they had had a personal computer, integral calculus might never have been invented. We have one, so we will use it to bypass most of the complications presented by calculus.

While we are philosophizing here I will explain one of the differences between this program and a standard college physics course. I make a distinction between knowledge and understanding. Knowledge involves gathering, remembering and organizing facts to get a result. Understanding involves gathering, remembering and organizing basic principles that may be used to generate facts in a wide variety of situations. The more you understand, the less you need to know.

Most physics courses are centered on exams and exams are centered on problem solving. There is nothing wrong with that by the way. You need those skills. But one of the consequences of this focus on high speed problem solving is that there is a great temptation to extract certain equations from the explanations, like x - x₀ = v₀ * t + 1/2 * a * t² and commit them to memory. Then at exam time select one or more of the equations and plug in the known quantities to get the unknowns. This is an efficient way to take exams but requires you to know a lot of information.

My purpose here is to strengthen your understanding of this material. We will look at the information we cover this way and that, turning it inside out sometimes, and finding links among the topics so that you develop real understanding. In this playing with the ideas there are few problems to solve and no exams but your ability to solve problems and take exams will be better for having the understanding. Beyond that, in the "real world", that place you go after college, you will have a much better shot with this understanding at solving problems no one has thought of before.

Now in spite of what I said about problem solving, let's return to the thread of the story with some examples of the use of the constant acceleration, 1 dimensional motion equations. We know from experiment that the acceleration due to gravity on a body is very nearly constant. The value of that constant near the surface of the Earth is approximately 9.8 meters per second per second.

In the first case consider simply dropping the ball from a window 10 meters above the ground. How long does it take to reach the ground? In solving problems the trick is in translating the words into quantities about which we know something. It looks like "dropping", "10 meters" and "reach the ground" are key bits of information. I interpret "dropping" to mean that v₀ is zero. If we let ground level be the origin of our reference frame, then x₀ is +10 meters. Since there is no mention of any other force on the ball, we take gravity to be the only motive force so acceleration is -9.8 meters per second per second. The minus sign because the acceleration is directed toward smaller displacement numbers. Finally "reach the ground" means that at the time we are solving for, x=0. Next, scan around for some relationship that relates v₀, x₀, a, x and t.

The formula x - x₀ = v₀ * t + 1/2 * a * t² seems to fit the bill. If we just plug in the values we are given, we get 0 -10 m = 0 * t s +1/2 * (-9.8 m/s²) * t s². This reduces to -10 m = -4.9 m/s² * t s². Notice that we are still OK with the units. So -10 m/(-4.9 m/s²) = t s², or t = ((10/4.9) s²)^.5 = 1.43 s to 3 significant figures. We reject the negative square root as not having any physical significance.

The process we just went through will work for any initial conditions of position or velocity, so balls thrown from the ground up, from a height down or from a height up, where the question is "how long to reach any condition?", work the same way just with different numbers. Physics professors are usually not content to ask questions in such a straightforward fashion. They like to ask things backwards, or sometimes even sideways.

Consider a ball tossed upward from our 10 meter window with an initial velocity of +20 meters per second (m/s). To what height does it rise above the ground, and what is its speed just before it hits the ground? Again extract the given data from the words. We get v₀=+20 m/s, x₀=+10 m and a=-9.8 m/s². Now we have to look in the question for additional information. There are two parts to the question. In the first part we want to know "to what height?" In the second part we want to know "how fast". Two part questions are usually best worked separately but you may have to use the answer to one part to get the other part figured out. If the questioner is particularly nasty, she may ask them in reverse order so you need to work the second part first.

So what do we know about the ball at the time of maximum height. Well, we know it isn't going any higher and will soon be going lower so the magnitude of its velocity must pass through zero at that instant. This is one of those statements that is obvious after you hear it but unless you have an intuition about the physics of a situation, you might get hung up for a long time trying to figure out that in the first part of the question, v=0 at the maximum height. Then you have to recognize that knowing that is worthwhile. The question asks "what height?", not "how long?". Here is where you need take what you can get if what you want is not readily available. Any information is preferable to none.

Since v = v₀ + a * t we can now find the time of maximum height, t = (v - v₀) / a = (0 - 20 m/s) / -9.8 m/s² = 2.04 s. Now we can use x - x₀ = v₀ * t + 1/2 * a * t², which after plugging in everything we know gives us x = 10 m + 20 m/s * 2.04S -4.9 m/s² * 2.04²S² = 10 m + 40.8 m - 20.4 m = 30.4 m.

Now that we know the height from which the ball is falling, we can use x = 1/2 * a * t² to get the time of the fall to be t = (2 * x / a)^.5 = (2 * (-30.4) / (-9.8))^.5 = 2.49 s. Then using v = a * t we can get the velocity at impact of v = -9.8 m/s² * 2.49 s = -24.2 m/s

I can sense that you are growing weary of all this algebra in the name of better understanding. I know I am. Wouldn't it be nice to have a mathematical model of the constant acceleration problem into which you could put initial conditions and out of which would come the answer to any required degree of precision. Well we just happen to have such a homework engine in our "Physics-1" program. If you are curious you may jump to the Physics-1 download site. You will still have to practice a lot of problem solving to be successful, but all that work gets in the way of understanding. In this program we will be looking to minimize the tedium.

As an alternative to the "Physics-1" program, we offer in this online edition a limited scope version of the constant acceleration model I mentioned above. In the Free Body Diagram display you may enter initial position, velocity and acceleration, and see the results displayed as a plot of position and velocity vs. time. Then using the cursor, you may get approximate values for many parameters. This tool will be available to you after we have a few more lessons under our belt.

Are there any questions?

In the next section we are going to cover some vector arithmetic to prepare ourselves to handle more than one-dimensional situations.