|
When everything that goes around, comes around...
|
This section of the course deals with a different way of
representing the laws of motion, based on the motion about some
fixed line. In the next section, called rotational dynamics, we
will build a model based on rotation, allowing you to predict the
future of rotating objects. In this section we will introduce the
parameters that describe rotation and cover enough of the basics
to help you develop some intuition about general motion of many
particle systems.
In the translational motion which we have been studying, every
particle undergoes the same motion. Now we will consider a kind
of motion which is fundamentally different. We will give the name
"rotation" to the motion of a solid object in which
every particle follows a circular path such that the center of
the circle that each particle traces lies on a straight line.
That line which contains the centers of each particle's
circular trajectory we will call the "axis of
rotation". The axis of rotation may pass through the object
or not.
The obvious difference between rotation
and translation is that in translation the object as a whole goes
somewhere, with no guarantee that it will ever come back. In pure
rotation it remains in the vicinity of the axis of rotation and
periodically returns to its original position. I use the term
"pure" rotation because it is possible that an object
undergo both translation and rotation simultaneously. This is
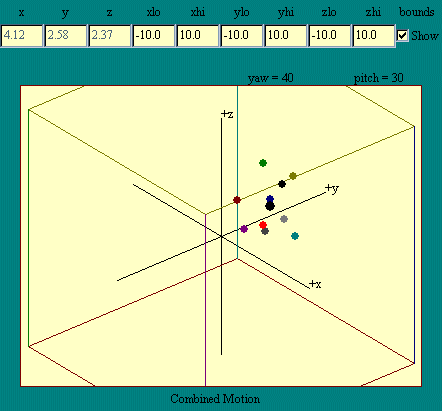
illustrated in the Combined Motion
display. In this display we have a solid object made up of ten
visible particles. Remember that being a solid means that the
particles maintain their original separations. Because this is a
computer model rather than a real object, we can also show the
center of mass of the object. It is the larger white spot.
|
|
|
What we will do next is develop the tools necessary to predict
the future of an object undergoing this sort of motion. A
different set of variables is used to describe rotation. The
displacement in translation was measured along the coordinate
axes, or as a distance and direction. In rotation we will measure
the angle from a reference line to the position of interest and
call it the angular displacement theta(the Greek letter q). Angular displacement is evidently a
scalar quantity since one number completely defines it. If the
reference line is the x axis, the angular displacement is the
angular position.
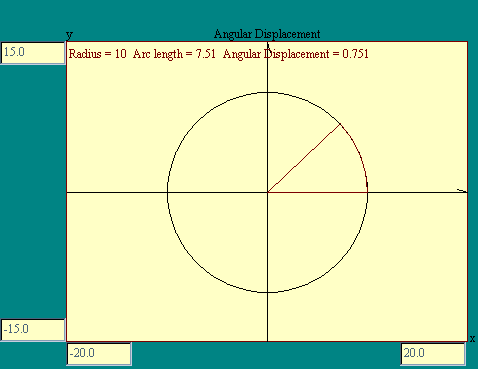
The units of angular measure will be
the "radian". A radian is the ratio or the length of
the arc cut by an angle, to the length of the radius of that arc.
See the Angular Displacement display for
an illustration. Since it is the ratio of two lengths, the radian
is unitless.
|
|
We also have measures in rotation analogous to velocity and
acceleration. Velocity in angular measure is the rate of change
of the angular position with respect to time, Dq/Dt. Since the angular position as we have
defined it is a scalar quantity, so is average the angular
velocity, being a scalar divided by another scalar, the
difference in time. The instantaneous angular velocity is the
limit as Dt approaches zero. We will
use the Greek letter omega, w, to
symbolize the instantaneous angular velocity.
 In thinking about angular velocity, we are
faced with one of the things that makes introductory physics
courses skip over much of the study of rotation. I argued
convincingly a while back that average angular velocity, Dq/Dt, was a scalar quantity. When we let Dt approach zero to get the instantaneous
angular velocity, the Dq becomes a vector. In fact it becomes a
vector pointing off in a direction not even in the plane in which
the rotation is taking place. It boggles the mind. In thinking about angular velocity, we are
faced with one of the things that makes introductory physics
courses skip over much of the study of rotation. I argued
convincingly a while back that average angular velocity, Dq/Dt, was a scalar quantity. When we let Dt approach zero to get the instantaneous
angular velocity, the Dq becomes a vector. In fact it becomes a
vector pointing off in a direction not even in the plane in which
the rotation is taking place. It boggles the mind.
Rather than interrupt our life at this point to ponder this
perversion, consider the following experiment to help you believe
that finite rotations behave differently than infinitesimal ones.
Take a beer stein and hold it with the handle to your right and
the opening facing upward. We are going to consider two kinds of
rotation of the stein. An "A" rotation will move the
opening directly away from you. A "B" rotation will
rotate the stein clockwise as you look down on it.
Now perform a 90-degree A rotation, followed by a 90 degree B
rotation. You should end up with the stein's handle toward
you and the opening to your right. Return the stein to its
original position and then give it a 90 degree B rotation
followed by a 90 degree A rotation. Now you see the handle on top
and the opening away from you. Evidently for large rotations the
order is important. For the mathematicians among you, the finite
rotation operators A and B do not commute.
Now repeat the experiment with 10-degree rotations. The
difference in the final positions in the two cases when the
rotation is small is well nigh undetectable. In the limit of
infinitely small rotations, the operators do in fact commute.
This does not prove that instantaneous angular velocity and
acceleration are vectors, but lends credibility that the
instantaneous values might be qualitatively different than the
average ones.
|

|
|
The average angular
acceleration is the rate of change of
Dq/Dt over some time difference so it too is a
scalar. The instantaneous angular acceleration is a vector
symbolized by the Greek letter alpha,
a.
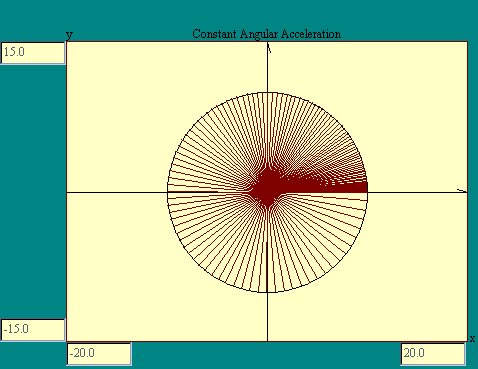
The
Angular Velocity and Acceleration
display shows the successive angular
displacement of an object undergoing constant angular
acceleration where a = 2 radians per
second squared, r/s2. The display shows 125 steps of
.02 seconds each, about enough to complete one revolution
starting from rest. Notice the angular displacement is larger in
each step as w increases.
|
|
Because of the way we have defined these angular terms, the
relationships among q, w and a are the
same as the relationships among x, v and a in translational
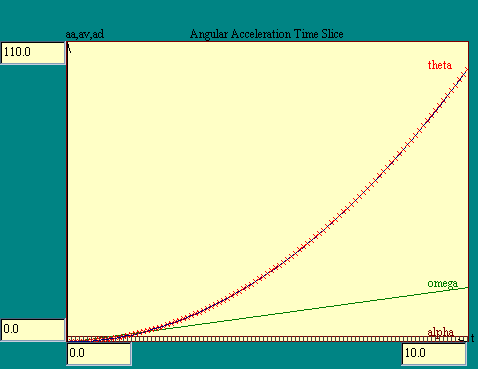
motion. The time slice techniques we developed in going from
acceleration to velocity to displacement also apply in going from
a to w to
q. The
Angular Acceleration Time Slice display illustrates this.
So... Let us consider the instantaneous angular velocity,
w, to be a vector whose magnitude is
the limit as Dt approaches zero of
Dq/Dt, and whose direction is given by the
direction of your right thumb when your right fingers curl in the
direction of the rotation of the object. I am not kidding. That
is really the way it is defined. Actually that choice of
direction does make a certain amount of sense since it coincides
with the axis of rotation. The axis of rotation is the only line
uniquely defining the orientation plane in which the rotation of
an object takes place.
The instantaneous angular acceleration,
a, which is the change in instantaneous angular velocity
divided by the time for that change, is of course a vector in the
same direction whose magnitude is the limit of Dw/Dt as the change in time approaches
zero.
Now let's look at a particle rotating in the (x,y) plane
about the origin at a radius r. The relationship of its angular
position to its displacement s along the arc of its circular path
is
s = r * q.
The definition of a radian is s/r so with
q measured in radians, this relationship comes directly
from the definition. A tiny change in s,
Ds, then would equal r times the corresponding tiny change
in q,
Dq. Dividing both sides of that
equation by the increment of time Dt
over which the changes take place we get
Ds/Dt = r * Dq/Dt.
But Ds/Dt
is just the velocity tangent to the circle and Dq/Dt is just w, so
the linear speed, v, of the particle is equal to the radius times
the angular speed so
vt = r *
w.
The same argument we just made for velocity holds for the
acceleration as well so the tangential component of a
particle's acceleration equals the radius times the angular
acceleration so
at = r *
a.
In the section on circular motion of a particle we found the
radial component of the acceleration of a particle in circular
motion of radius r to be vt2 / r which in
terms of angular quantities is
ar = (r *
w)2 / r .
So now we have equations relating each of the linear quantities
to the angular ones.
|
|
|
Now if you have been paying close attention, you may have
noticed that I seem to have talked myself out of the necessity
for introducing the angular quantities at all. It seems that we
can express even circular motion of a particle by use of the
linear quantities. The real reason for the angular quantities is
that different points in a rotating body may have different
linear displacement, velocity and acceleration. In a body
rotating around a fixed axis, each point, and therefore the body
as a whole will have the same angular displacement, velocity and
acceleration. By use of the angular quantities the motion of the
whole body may be described in a simple way.
So far we have developed the necessary tools to describe
rotation. Now we will work on what causes rotation. In the case
of translation we associated a force with the linear acceleration
of an object. In rotational motion, what quantity should we
associate with angular acceleration? It must be something other
than simple force because the same force, depending on where it
is applied will produce different angular accelerations. Think of
trying to push open a heavy door by exerting a force near the
hinge. The same force applied at the doorknob might work just
fine.
The rotational quantity corresponding to force is
"torque". Let's begin by thinking about a single
particle. If a particle is located at a position given by a
vector r, relative to our frame of reference and a force
f acts on that particle, the torque, Greek letter tau
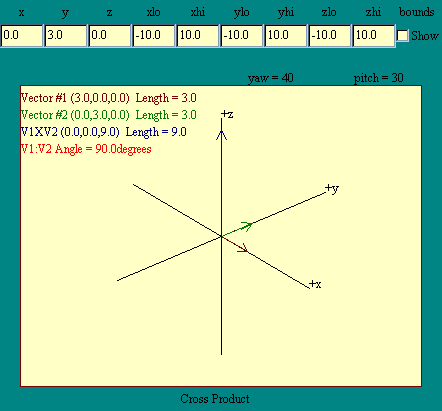
t, is defined to be the cross product
of the vector r with the force f,
t = r X
f .
Torque then is a vector quantity whose magnitude is given by the
magnitude of r times the magnitude of f times
the sine of the angle between r and f. The
direction of the torque vector is given by the right hand rule as
described in the Vector Arithmetic section. Rerun the Cross Product display to review this.
|
|
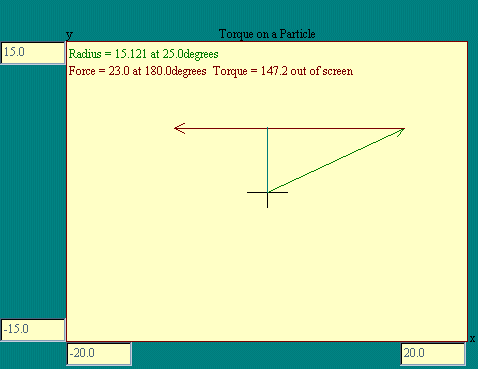
To help get a grip on the effect of
the position vector r and the force vector f on
the resulting torque on a particle, let's set up a reference
frame with the (x,y) plane being the plane defined by the two
vectors, r and f. Then torque will be directed
along the positive or negative z direction. This situation is
illustrated in the Torque on a
Particle display.
 Torque used to be a confusing concept for
me. Here are some of the things that bothered me about it. Notice
that the units on torque are force times distance. These are the
same units that we attached to work in the case of translational
motion. Torque and work though are two different physical
quantities. One obvious difference is that torque is a vector and
work is a scalar. Torque used to be a confusing concept for
me. Here are some of the things that bothered me about it. Notice
that the units on torque are force times distance. These are the
same units that we attached to work in the case of translational
motion. Torque and work though are two different physical
quantities. One obvious difference is that torque is a vector and
work is a scalar.
The vector nature of torque is another issue. Why a vector?
And for that matter, where a vector? In our display the torque
either points straight out of the screen if positive and straight
in negative. In other words, straight along the z Axis. So its
magnitude and direction are fixed but what about its location.
Customarily we see the torque vector drawn at the origin of the
r vector so it is visually more associated with the
reference frame than with the particle, still we say it is the
torque on the particle. Of course the rest of the story is, that
it is the torque on the particle... about the chosen origin. Both
the location of the particle and the choice of the axis of
rotation affect the torque.
And another thing. The torque vector does not point in a
direction in which anything is happening The force, the radius
and the motion are all in the (x,y) plane. Why does the torque
refuse to cooperate and insist on running at right angles to
everything else?
It is best for now to let go of these troubling issues and
press on with the study of rotation. Let us for the moment accept
that it is torque which produces rotation of a particle about an
axis and not stew about the perverse vector nature of the
thing.
|
|
|
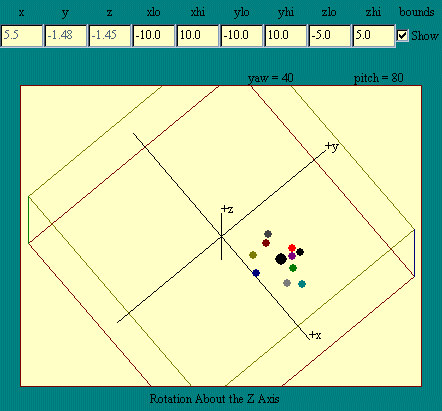
In the combined motion display,
the rotation was about an axis parallel to the z-axis and passing
through the center of mass. Other lines could serve as the axis
of rotation. Run the Rotation About the Z
Axis display for one example.
You might observe that rotation about an axis not passing
through the object begins to look like the translation - rotation
motion combined, except that the translation is in a circular
path. The distinction between translation and rotation is really
about whether the object travels in a circle comes back during
the time of our observation. In the rotation about the z axis
case, it may, so we call that rotation.
Since each particle moves around its orbit with constant
speed, the angular acceleration is zero so evidently the torque
applied to the object must also be zero since any torque results
in angular acceleration. Does this imply that the particles of
the system or the system as a whole experiences no external
force? Clearly not the case. The center of mass of this system
follows a circular path so the object as a whole must be subject
to a force. Otherwise it would fly off in a straight line. What
the zero torque condition tells us is that the direction of the
force on each particle in the system is exactly towards the z
axis.
|
|
What if we tried to describe the motion of this object where
the torque and angular measures were taken about some arbitrary
point in the object, say one of the particles for example? Well
in theory we could write expressions relating torque to angular
acceleration in such a system. The problem with an arbitrary
point as a reference for angular quantities is that the motion of
the point itself can be quite complicated. It may be rotating
about any combination of three axes and also translating, not to
mention vibrating. This is going to make a real mess out of
anything measured relative to such a point.
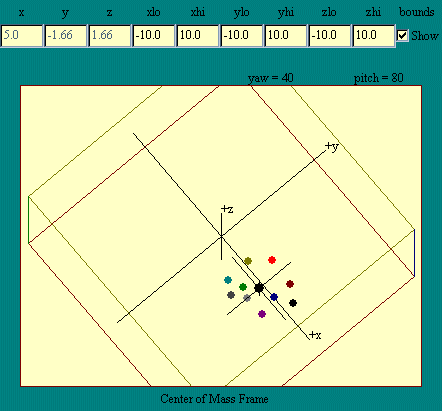
There is a point in a collection
of particles which is not as badly behaved as an arbitrary point.
That is the center of mass. Lets place a little reference frame
at the center of mass and picture the movement of our collection
of particles in that reference frame. Since this frame travels in
a circular path, it is not an inertial reference frame but for
purposes of this demonstration that is not an issue. We will deal
with non-inertial reference frames in the run-time book,
Physics_T. The
Center of Mass Frame
display adds the
center of mass frame to the previous display, with the
orientation of that frame fixed in the larger reference frame. In
discussing the previous display we said that the net torque was
zero. Does that mean that the object is not rotating around the
center of mass as it rotates about the z-axis? Have that question
in mind as you play with this next display.
|
|
|
As you can see, motion of the object includes its travel
around the z axis and a secondary rotation relative to the center
of mass frame of reference. In this instance these two rotations
are synchronized so as to keep the same side of the object always
facing the origin of the reference frame. Like the Moon in its
orbit around the Earth. If the object was not rotating on its own
axis, as we view it from the reference frame origin it would
appear to be rotating once per the period of its orbit around the
origin.
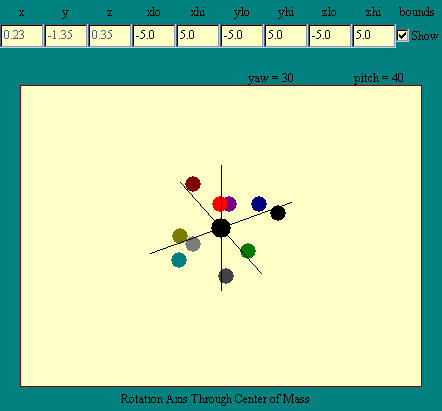
Suppose we were observing the
object in the reference frame with its origin at the center of
mass. Then we would only see the rotation about the object's
axis as shown in the Rotation Axis Through
Center of Mass display.
Any motion that a rigid object undergoes may be resolved into
motion of the center of mass and rotation about the center of
mass. Forces that act through the center of mass contribute
nothing to the rotation about the center of mass since the torque
produced by such forces is zero. Other forces may contribute to
both rotation and translation. In the next section on rotational
dynamics, we will work out some of the details.
Are there any questions?
|

 Next
Next
 Previous
Previous
 Other
Other
|




