|
|
|
|
The inner workings and hidden mechanisms of the wheel...

|
In the previous section of this course we
established certain quantities useful in describing rotation.
Angular displacement q measured in
radians is analogous to linear displacement measured in meters.
Angular velocity w measured in radians
per second is analogous to linear velocity measured in meters per
second. Angular acceleration a
measured in radians per second squared is analogous to linear
acceleration measured in meters per second squared. Torque t measured in Newton meters is analogous to
force measured in Newtons. These angular quantities are not equal
to their linear counterparts either numerically or in units but
they play similar roles in rotational dynamics.
In linear dynamics, we noticed that the ratio of force to
acceleration had a physical significance. It was the mass of an
object. In rotational dynamics, the ratio of torque to angular
acceleration has a similar significance. It is the moment of
inertia of the object. The mass of an object is simple. It
depends only of the amount of stuff in the object. The moment of
inertia depends not only on how much mass an object has but also
the shape of the object and the choice of the axis about which
the moment of inertia is measured.
|
|
Consider the ratio of torque to angular acceleration for a
single particle in circular motion of radius r about the
origin of our reference frame. The particle is subject to a
radial force which keeps it in the circular path, and a
tangential force ft which provides the
angular acceleration. The torque resulting from
ft is just ft * r
since the angle between a tangential force and the radius is 90
degrees so the sine factor in the cross product is 1.
The force ft may be written as the product of
the tangential acceleration, at and the mass,
m, of the particle according to Newton's second law. But we
know already that at is ra, so
t =
ft * r = (m*at) *
r = (m * ra) *
r = (m * r2) *
a.
The ratio of t /
a then is the quantity (m * r2). This
is the moment of inertia, I, of a particle. It plays the role of
mass in rotational dynamics.
For objects made up of many particles, the moment of inertia
is the sum of all the moments of inertia for the individual
particles. Real objects are indeed made up of many particles, so
many that treating them individually is a hopeless task. We can
imagine the object to be divided up into small volumes that can
be treated as particles and then sum the moments of inertia over
these small volumes. Mathematically this summing up is
accomplished through integral calculus.
The general approach to calculating a moment of inertia for an
object of complicated geometry about an arbitrarily chosen line
is a mathematical exercise that we do not need to go
into at this point. In fact for most real objects the calculus is
too hard for anyone. If a moment of inertia must be determined,
either a computer technique called finite element analysis is
used or if the object is not too large, we may measure the moment
of inertia, I, by applying a known torque and measuring the
angular acceleration.
|

|
|
For a hollow cylinder where the walls are of significant
thickness, you may imagine that half the mass is in a hoop at the
outer radius and the other half the mass in a hoop at the inner
radius so that
I = M/2 * (R12 +
R22).
It might help you to visualize this situation by starting with
the two hoop configuration and imagining taking a bit of mass
from the outer hoop and forming a new hoop slightly inside the
outer. This would decrease the moment of inertia. Then take an
equal amount of mass from the inner loop and form a loop outside
the inner, just far enough to restore original moment of inertia.
If you continue this process you will find that you can fill the
space between the inner and outer radius and maintain the
original moment of inertia. A solid cylinder is just a hollow
cylinder where the inner radius is zero so
I = M/2 * R2
for the solid cylinder or disk. Notice that in our discussion of
cylinders, the height of the cylinder does not have any effect,
except to the extent that the mass is effected by a tall cylinder
as opposed to a flat disk.
|

|

|
A thin rod of length L rotated about one end is just a
collection of particles each of mass
DM at radii ranging from zero to the length of the rod.
The contribution to the moment of inertia of a particle at
distance r, from the origin is
DI = DM*r2.
But DM can be expressed as the mass
per unit length of the rod, m, times a little length element,
Dr. so
DI = m *
r2 * Dr , or DI / Dr = m *
r2.
This means that the rate of change of I with respect to r is m *
r2. Remember that the rate of change in the limit as
Dr becomes very small is the
derivative of I with respect to r. To find the function I(r)
which describes the moment of inertia as a function of the
variable r, we need to find a function whose derivative is m *
r2.
Thinking back to our discussion of the derivative of the
quadratic function, in the section on rates
of change , we found that if y=a*xn, the
derivative of the y with respect to x,
Dy / Dx, was
n*a*x(n-1). In this case
DI / Dr = m * r2.
To pick out the function which has this expression as its
derivative, just increase the exponent by 1 and divide by the new
exponent. This trick is called taking the anti-derivative of m *
r2 and gives us m/3 * r3. So
I = m/3 * r3
for any r. Notice that the total mass of the rod is m * r, so
I = M/3 * r2
and for a rod of length L,
I = M/3 * L2.
Now what would happen if we rotated the rod about its center
rather than about one end. That would be equivalent to having two
rods rotated about their ends, each of half the length of the
original. The moment of inertia of a rod of length L/2 rotated
about its end would be (1/2*M)/3 * (L/2)2, based on
the result above. This reduces to 1/24 * M * L2. Of
course there are two such half rods, so the total moment of
inertia for a rod rotated about its center is
I = M/12 * L2.
|
|
In finding the moment of inertia of a rod about two different
axes, we have happened upon an important principle called the
parallel axis theorem. The theorem states that if an object has
moment of inertia Icm about its center of mass, like
the rod in the second case, then its moment of inertia about any
axis parallel to the original axis of rotation is Icm
+ M*D2, where D is the distance between the parallel
axes,
I = Icm + M * D2.
Let's check this with the rod example. D in this case was
L/2. Icm was M/12 * L2. So
I = M/12 * L2 + M *
(L/2)2 = M*(1/12 + 1/4)*L2 = M*(1/12 +
3/12)*L2 = M/3 * L2.
A rectangular plate of mass M and dimensions a by b has a moment
of inertia about its center of mass the same as if all its mass
were located in a rod whose length was the diagonal of the plate.
The length of the diagonal is the square root of (a2 +
b2), so the moment of inertia is
I = M/12 * (a2 + b2)
.
Without going through the mathematics for the hollow sphere and
solid sphere, I will just state the moment of inertia about a
center of mass axis for each. For the hollow sphere,
I = 2*M/3 * L2.
For the solid sphere it is
I = 2*M/5 * L2.
Now if we have an object of one of the shapes we know about,
we can calculate the angular acceleration about any axis parallel
to the axis of symmetry, from the torque about the given axis.
All we need to do is divide by the moment of inertia. In
analyzing the motion of solid objects, those with significant
dimensions as opposed to a particle, we need to pay attention not
only to the magnitude and direction of the forces, but also to
where on the object they are applied. On the Disk Research
display at the end of this section, we will demonstrate this.
Before we get to that however, we need to develop some additional
rotational dynamics ideas.
|
|
|
Getting back to our
particle in the (x,y) plane at position r. Suppose that
the particle has linear momentum in our reference frame of
pkgm/s. The "angular momentum" of the particle
about the origin is defined as L = r X
p. Only the component of p perpendicular to
r contributes to the angular momentum. Let's consider
two particular instances of angular momentum about the origin of
a particle.
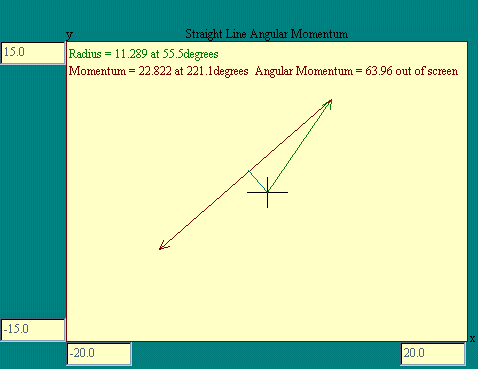
If a particle is moving at a constant velocity in a straight
line in our reference frame, can it have an angular momentum?
Look at the Straight Line Angular
Momentum display for an illustration.
The other particular instance of angular momentum of a particle
about the origin we should discuss is that of a particle in
uniform circular motion around the origin. In this case the
linear momentum p is always perpendicular to the radius
vector r so
L = |r| * |p|.
But |p| is m * |v| so
L = m * |r| * |v|.
In terms of angular quantities, |v| = |r|*w so we now have
L = m * |r| * |r| * w.
So for circular motion of a particle, the angular momentum is
L = I * w,
which is exactly analogous to the linear momentum being mass
times velocity.
|
|
Now I want to derive a connection between the torque and the
angular momentum; a topic of vital importance in safe operation of large rotating machinery.
Remember that the force f=Dp/Dt
where p is the linear momentum. Let's take the cross
product of r with both sides of that equation so that
rXf = rX(Dp/Dt).
But rXf is just the torque
t so
t =
rX(Dp/Dt).
Next, go back to the definition of angular momentum, L
= rXp and take the derivative with respect to
time of both sides. Remember that the derivative is just the rate
of change of the variable where the time interval over which the
change happens approaches zero. That is the change in the
variable divided by the tiny time over which the change took
place. So
DL/Dt =
D(rXp)/Dt.
 OK so how do we get the rate of change in
the cross product rXp in terms of the
individual factors r and p. We might be tempted
do distribute the D among the factors,
making D(rXp)/Dt =
Dr/Dt X Dp/Dt .
That makes the assumption that the derivative of a cross product
is the cross product of the derivatives, which turns out to be a
bogus assumption. Just look at the units on each side of this
expression. We have m2kg/s2 on the left and
m2kg/s3 on the right. Evidently we need to
look at this in more detail. OK so how do we get the rate of change in
the cross product rXp in terms of the
individual factors r and p. We might be tempted
do distribute the D among the factors,
making D(rXp)/Dt =
Dr/Dt X Dp/Dt .
That makes the assumption that the derivative of a cross product
is the cross product of the derivatives, which turns out to be a
bogus assumption. Just look at the units on each side of this
expression. We have m2kg/s2 on the left and
m2kg/s3 on the right. Evidently we need to
look at this in more detail.
The change in the cross product with respect to time is
D(rXp)/Dt =
((r +
Dr)X(p +
Dp) - rXp) / Dt.
Next we carry out the multiplications indicated by the cross
products remembering that the order in which we place the factors
matters. That gives us
D(rXp)/Dt =
(rXp +
DrXp + rXDp +
DrXDp -
rXp) / Dt.
The rXp and the -rXp terms
cancel out and the DrXDp term, being the product of two
very small numbers may be considered zero as
Dt approaches zero. That leaves us with
D(rXp)/Dt =
(DrXp +
rXDp) / Dt,
or
D(rXp)/Dt =
Dr/DtXp + rXDp/Dt.
But Dr/Dt is just the particle velocity v
and p is m*v so
Dr/DtXp = vXm*v =
0
because the v and m*v point in the same
direction and parallel vectors have a zero cross product.
This leaves us with the rate of change of the particles angular
momentum,
DL/Dt = rXDp/Dt =
t.
The rate of change of angular momentum equals the torque just as
the rate of change of linear momentum equals the force. This
tells us that if the torque on an object is zero, then the
angular momentum remains constant. This is the principle of the
conservation of angular momentum, which has far reaching
consequences, extending to quantum mechanics even though we
discovered it in the realm of classical mechanics.
|

|
|
To
calculate the total angular momentum of a system of particles we
must add up the angular momentum of each of them about the same
point. For that point we choose the origin of our reference
frame. The angular momentum of each is a vector so the total
angular momentum is the vector sum. For a system of n particles
we have
L = L1 +
L2 + ... + Ln = 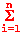 Li.
Li.
As time passes, the total angular momentum about the origin may
change if a net torque exists. We know that the forces
experienced by the particles in an object may be internal forces,
forces among the particles in the object or external forces,
those applied to the particles in the object by some outside
agent. Newton's third law tells us that the force between any
pair of particles is equal and opposite on each of them and is
directed along the line joining them. In this case the internal
torques are all zero since the forces are collinear. So
DL/Dt = t,
where t is the net external torque.
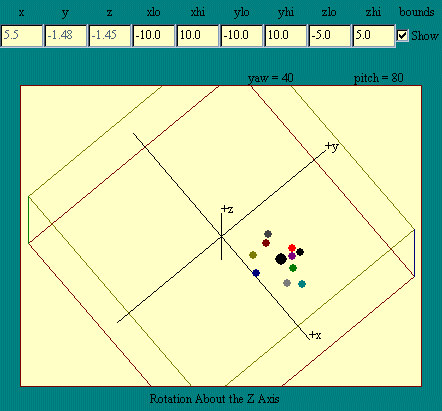
Let's take another look at the
Rotation About the Z Axis display.
Since each particle moves around its orbit with constant
speed, the angular momentum of each particle and therefore of the
system as a whole is constant. Constant angular momentum means
that the net external torque on the system is zero. Any external
force then must not have a tangential component so the net
external force points toward the z-axis. This is the same
conclusion we reached in talking about angular acceleration, but
in this instance we arrived at the conclusion from the standpoint
of angular momentum.
|
The analogy between linear dynamics and rotational dynamics
extends to the ideas of work and energy also. Kinetic energy of
rotation, ker, is the sum linear kinetic energy of all
the particles involved. Suppose we have a solid object rotating
with angular velocity w. Any particle
in the object, say the ith one, will have kinetic energy
kei = 1/2 * mi *
vi2.
The vi factor can be expressed as
vi = ri * w so
kei = 1/2 * mi *
ri2 *
w2.
For the whole object the rotational kinetic energy is
ker = 1/2 * 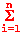 mi *
ri2 *
w2.
But mi *
ri2 *
w2.
But 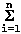 mi * ri2 is just the
moment of inertia, I, so
ker = 1/2 * I * w2,
just as you would expect from your knowledge of linear dynamics.
mi * ri2 is just the
moment of inertia, I, so
ker = 1/2 * I * w2,
just as you would expect from your knowledge of linear dynamics.
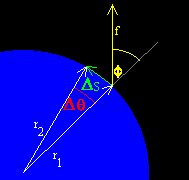
Let's use the picture at the right to understand
how a force applied to a solid object free to rotate about a
fixed axis, results in work being done. Here we see a solid blue
disk with its center of mass at the origin in the (x,y) plane. A
white radius vector is painted on the disk. A force is applied at
the circumference of the disk, indicated by a yellow vector. The
force vector makes an angle f with the
radius vector. After a short time, the applied force will rotate
the disk to a new position, moving the radius vector from
position r1 to position
r2. The angular displacement is Dq. The distance
through which the force f was applied is the arc length
Ds.
|
|

|
The bit of work DW done in angular
displacement Dq is f · Ds. The arc length
Ds may be replaced by the quantity |r|*Dq as long as
Dq is
small. The dot product of the force vector with the vector
|r|*Dq is
the product of the magnitude of |r|*Dq and the
magnitude of the component of f in the direction of
|r|*Dq.
That component of f is |f|*sin(f). So we have
DW = |f|*sin(f)*|r|*Dq .
But we know that the quantity |f|*sin(f)*|r| is the torque produced by f
about the origin, on the disk. So
DW = t*Dq .
This result is consistent with the expression for work in linear
motion, being the product of force times displacement. In
rotation torque plays the role of force and
Dq plays the role of
displacement.
In linear motion we found a work-energy theorem that proved
useful in predicting the future of a moving object. In rotation
we can get a similar relationship. We will begin with
Newton's second law expressed for rotation of a symmetrical
solid body rotating around its axis of symmetry,
t = I * a = I * Dw / Dt .
 Now we are going to use a trick that tends
to make students say, "How did you know to do that?".
We are looking for a relationship between work and energy and we
have just discovered that work involves torque and displacement,
like this: Now we are going to use a trick that tends
to make students say, "How did you know to do that?".
We are looking for a relationship between work and energy and we
have just discovered that work involves torque and displacement,
like this:
DW = t*Dq..
But our expression for Newton's second law does not involve
displacement, Dq. To introduce
Dq into our equation we can
multiply the right side of the equation by
Dq /
Dq, in effect multiplying the
right side of the equation by 1, which leaves it unchanged. The
result is,
t = I * (Dw / Dt) * (Dq / Dq) .
Now looking at the product of the two fractions, (Dw / Dt) * (Dq / Dq), notice that we can associate the
denominators with the opposite numerators so we get,
t = I * (Dw / Dq) * (Dq / Dt) .
But Dq /
Dt is just
w, so
t = I * w * Dw / Dq.
Now multiplying both sides of this equation by Dq we get
t * Dq = I * w * Dw = DW.
Then dividing by Dw we find
DW / Dw = I * w,
which says that the rate of change of work with respect to
angular velocity is the moment of inertia times the angular
velocity.
To get work as a function of angular velocity from the rate of
change we use the anti-derivative trick introduced earlier.
W = 1/2 * I *
w2.
So as w goes from and initial to final
value, the amount of work done is
W = 1/2 * I *
wf2 - 1/2 * I *
wi2,
meaning that the net work done by external forces in rotating an
object is equal to the change in the objects rotational kinetic
energy.
|
|
Although the measures of rotational dynamics were carefully
developed to parallel their counterparts from linear dynamics,
the analysis of rotary motion in the most general case is beyond
the scope of this course. We have to limit our analysis to a few
simple situations. We can only handle the rotation of solid
objects that have an axis of symmetry, rotating about an axis
that is parallel to one of the primary axes of the reference
frame. In addition the axis of rotation must be fixed in space
(spinning motion) or moving in a straight line as in the case of
a cylinder rolling along a surface (rolling motion). Even with
these restrictions you will find many commonly occurring examples
of rotation posed as problems in your physics textbook.
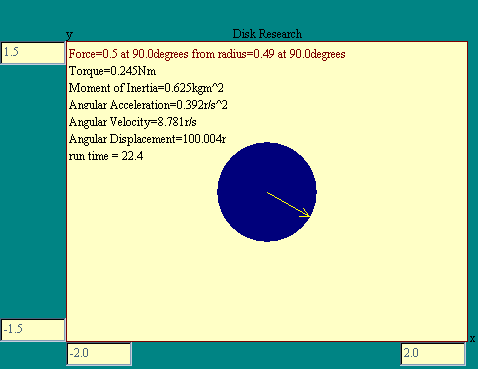
 I
suspect that at this point you have had enough of algebra and
anti-derivatives. To bring these ideas together, take a look at
the Disk Research display. I
suspect that at this point you have had enough of algebra and
anti-derivatives. To bring these ideas together, take a look at
the Disk Research display.
The point of discussing this different way of formulating the
laws of motion is to help you visualize the motion a system of
particles might undergo. To completely describe its motion we
might want to treat its rotation using some of the concepts here.
There is one additional kind of motion we will cover and that is
vibration. Not only might a system be translating and rotating
but also quivering in some fashion. In the next section of the
course we will look at this.
Are there any questions?
|
|

 Next
Next
 Previous
Previous
 Other
Other
|
|
|
|




