|
Its hard to get
a grip on this stuff..
|
Somewhere along the line you have probably been introduced to
the idea of three states of matter, solid, liquid and gas. Every
living person has experience with all three states. The objects
that we find in our surroundings include solids like rocks,
chairs and houses, the water we drink is liquid and the air we
breathe is gas. From this experience we have some intuition about
the distinction among these three. Solids have a definite volume
and shape, liquids have a definite volume but not shape and
gasses have neither a definite volume nor shape. That intuitive
distinction will be precise enough for now.
There is another characteristic that separates solids from the
other two states of matter. Solids can support shear stress, as
we discussed in Equilibrium and
Elasticity. Neither liquids nor gasses can. Those materials
that do not support shear stress are called fluids. Fluid
mechanics is the study of such materials and includes those
materials that we intuitively regard as liquids and gasses. There
are a few oddball materials where the ability to support shear
stress depends on how rapidly the stress is applied. Glass for
instance is fluid over very long time frames. Silly putty is
solid with regard to very short time application of shear stress.
We will not be treating these pathological cases in this
course.
Fluid mechanics is divided into statics and dynamics. Fluid
statics deals with the behavior of fluid essentially at rest in
our reference frame. Fluid dynamics deals with fluids in motion
or objects moving through stationary fluids. We will begin with
some ideas from fluid statics. Notice that in fluid mechanics we
begin talking about materials rather than objects. Up to this
point in this course we have dealt with particles either
individually or in relatively closely coupled groups. Now we are
going to back away from the behavior of individual particles and
tight groups of particles and begin to consider fluid materials
as an environment in which particles and other solids may find
themselves. The interaction between the materials as a whole with
other objects is the focus of fluid mechanics. Of course the
behavior of fluids is determined by the behavior of the particles
that make them up, but we will in general not pry into the
private lives of individual particle, just consider how the whole
society of particles behaves in fluids.
|
 |
 |
One of the properties of substances that influences fluid
mechanics is density, the mass per unit volume. Density in SI
units is kg/m3. Solids and liquids have densities in the range
of about 5e2 to about 2e4 kg/m3. The density of a solid or
liquid depends slightly on temperature, generally decreasing as
temperature increases, but remain in the stated range under any
reasonable temperature. The density of a gas of course is not as
fixed as for solids and liquids since we defined a gas as a
substance without a fixed volume and density involves the volume
of the material. The image at the left is a computer generated
map of the density of inter-stellar gas in a binary star system.
So that we can still talk about the density of a gas, we refer
it to a set of standard conditions called STP for standard
temperature and pressure. Those conditions are a pressure of one
atmosphere and a temperature of zero degrees C. Under these
conditions gas densities range from about 1e-1 to about 2 kg/m3.
The fact that gas densities at STP are about 1/1000 the density
of liquids and solids implies that the particles in the gas are
separated by about 10 times the separation in the liquid and
solid case. The density data also indicates that the difference
between solids and liquids may depend on something other than
simple the separation between the atoms or molecules making up
the substance.
|
| There are two important consequences of the fact that fluids
do not support shear stress. Firstly the only force that a fluid
can exert on an object submerged in it is a force everywhere
perpendicular to the surface of the submerged object. That is the
reason that spherical vessels are favored for deep submergence.
The compressive force is uniformly distributed over the whole
sphere. Secondly, the force exerted by a fluid at a particular
depth is felt uniformly in all directions. This is really the
first situation looked at from the point of view of the fluid
rather than the object.
The pressure exerted by a fluid at a particular depth, h, is
defined as the force per unit area that the fluid exerts on an
object submerged to that depth. As we will show shortly, the
pressure depends on depth, P=P(h) so to get the total force on
any finite surface other than a horizontal one, we must define
the pressure on an infinitesimal surface area, P(h)=Df/DA, where
Df is the little increment of force on
the area DA and DA is made as small as necessary so that the
variation in depth can be ignored. Then the force on the finite
surface area is found by adding up all the little Df's.
This should begin to remind you of the rate of change
discussion. The rate of change of force with respect to area is
P(h) so Df = P(h)*DA. To add up all the little Df's we can slice the depth of the finite surface
up into horizontal slices of constant depth, multiply the area of
each slice times the pressure at that depth and add up all the
products. The units on pressure being force divided by area are
newton/m2. The newton/m2 is given the name pascal(Pa)
1Pa=1N/m2. The standard atmospheric pressure, mentioned above,
is 1.013e5 pascals.
|
 |
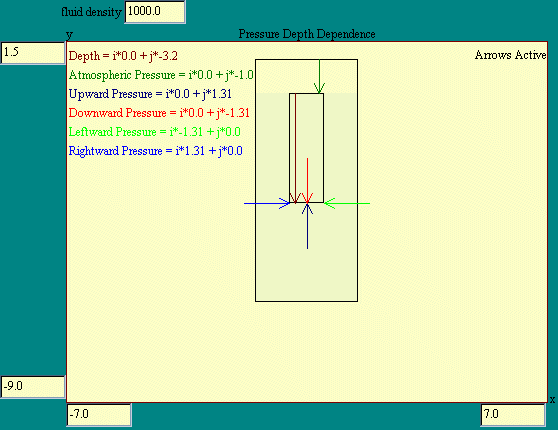 |
To get at the variation of pressure with depth, the P(h)
mentioned above, we are going to introduce a trick that your will
see again in different contexts. Suppose there is a container of
liquid and imagine a cylinder of cross sectional area A extending
from the surface of the liquid to a depth h. This cylinder is an
imaginary construct. It is there only in our minds, to form a
boundary between the sample of liquid we wish to consider and the
remaining liquid. This situation is shown in the pressure depth dependence model.
The weight of the fluid in the imaginary cylinder exerts a
force on the bottom face. Let's call the pressure exerted by the
weight of our sample of fluid on the bottom face of this
imaginary cylinder, P. There is also a pressure, P0,
exerted on the top of our imaginary cylinder by the weight of all
the air above it. Because the fluid is not flowing, we know that
it is in equilibrium. This means that the sum of the forces on
any cylinder of fluid must be zero. The upward pressure on the
bottom of the imaginary cylinder therefore must also be P +
P0.
The weight of the fluid in the cylinder is the density,
r, of the fluid times the acceleration
due to gravity times volume, w=r*g*V.
But the volume is A*h so the downward force on the bottom face of
the cylinder due to the weight of the fluid is r*g*A*h. The total force at the bottom of the
imaginary cylinder is
P0*A + r*g*A*h.
Dividing through by A, we find
P = P0+r*g*h.
indicating that pressure is indeed a function of depth.
|
| Suppose we want to find the total force on the vertical face
of a dam of height H and width W. Since the pressure depends on
depth, one approach would be to imagine the dam as a series of
horizontal strips of height Dh and
width W, where Dh was small enough
that the pressure variation from top to bottom could be
neglected. Then we could calculate the force on each strip and
add them all up. This is a good job for a computer.
In the case of our dam, we can use the P(h) to calculate the
total force. The force on each little strip is
Df = P(h)*W*Dh = (P0+r*g*h)*W*Dh.
If Dh is small enough, the total can
be found by finding the anti-derivative or integral of
Df. Remembering the trick for getting
the anti-derivative by increasing the exponent of the variable by
1 and dividing by the new exponent, we find
f = P0*h*W+1/2*r*g*h2*W
where we have made use of the fact that the sum of all
Dh is h. This technique works even if
the W is not constant but depends on depth as long as W(h) can be
written in a mathematical expression.
Because the dam has such a simple geometry and the pressure
varies linearly with depth, there is another way to get the total
force. We know the average pressure on the dam is
1/2*(P0+r*g*h). If we
multiply this average pressure by the area of the dam we will get
the total force
f = P0*h*W+1/2*r*g*h2*W
These three approaches to the same problem illustrate a very
general principle in the relation of physics to mathematics. The
greater the symmetry of a problem, the more likely we will be
able to solve it by elementary means. For a rectangular dam we
can just use algebra. If the dam had a face shaped like a
triangle, we could use calculus. If the dam had a face shaped
like the walls of a canyon the computer approach would be
best.
In fact we could always use the computer, but if we did we
would soon loose our understanding of the situation and only keep
the knowledge of what buttons to push. Replacing understanding
with knowledge is never a good idea. Then you would not recognize
the similarity between a dam and a hot air balloon and have to
start all over again to figure out how tough the balloon's fabric
would have to be to support the total force. Besides, you want to
be the person instructing the computer how to solve the
problem.
|
 |
 |
Notice that in the dam problem we carried the P0
term throughout. In fact since the dam will have atmospheric
pressure on its dry side as well as its wet, the dam design does
not have to include this term. It must only be strong enough to
support f = 1/2*r*g*H2*W. The
pressure including the atmospheric pressure is called the
absolute pressure. The pressure without the atmospheric pressure
term is called "gage pressure". It is the pressure that would be
measured on a normal pressure gage that detects the difference
between the pressure measured and atmospheric pressure.
The way we handled atmospheric pressure in our treatment of
the dam problem has hidden in it an assumption that pressure
applied at the surface of a liquid is felt throughout the liquid,
undiminished by distance, and the pressure is transmitted to the
walls of the liquid container. This may seem obvious but in 1650
AD it was a novel idea, first formalized by Blaize Pascal and
hence known as Pascal's law. The whole physics of hydraulics
derives from that idea.
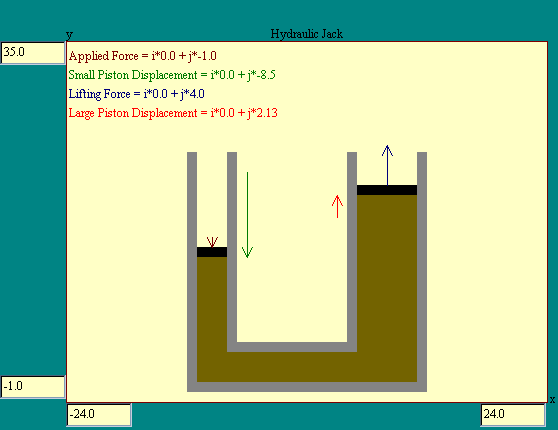
Consider a liquid container with two movable pistons forming
part of the pressure boundary, one large and one small. Applying
a force to the smaller piston will increase the pressure in the
liquid by an amount equal to the applied force divided by the
area of the smaller piston. This increased pressure will be felt
at the larger piston where the resulting force will be the
applied pressure multiplied by the area of the larger piston. The
ratio of the applied force to resulting force will be the ratio
of the large piston area to the small piston area. Run the
hydraulic jack model to see how this
works.
Of course another consequence of Pascal's law is that in a
container of liquid that is open to atmosphere at several
locations we will find the liquid surface at the same height in
each opening regardless of the size of the opening or the shape
of the container in the vicinity. In the absence of differences
in applied pressure liquid seeks it own level.
|
| Now let's consider a cube of solid stuff placed in a
container of liquid so that it is completely submerged. Since the
cube and the liquid cannot occupy the same space at the same
time, the volume of the cube displaces some liquid. Since liquids
are essentially incompressible the total liquid volume remains
the same. Since the volume occupied by the cube is no longer
available the displaced liquid must go elsewhere. The walls of
the container prevent it from going out to the side so it must go
up. In effect pushing the cube into the liquid lifts the
displaced liquid. The force required lift the displaced liquid
must come from the pushing of the cube into the liquid.
The weight of the displaced liquid, wl is its
density, rl, times the
displaced volume, Vl, times the acceleration due to
gravity, g.
wl = rl*Vl*g
The force wl must be provided by the force on the cube
of stuff. This force is a combination of the weight of the cube
and any applied force either up or down. The weight of the cube
is its mass times the acceleration due to gravity. The mass is
the density of the stuff, rc times its volume, Vc, so
the weight comes out to be
wc = rc*Vc*g.
If the weight of an object is greater than the weight of the
displaced liquid the net force on the object will be downward and
the it will sink. If the weight of an object is less than the
weight of the displaced liquid, the net force on the object will
be upward and it will rise. The weight of the object is fixed but
the weight of the displaced liquid depends on how much of the
object is submerged. If the entire object is submerged and still
the weight of the displaced liquid is less than the weight of the
object, it will accelerate downward until the excess object
weight is supported either by the force of friction as the object
moves through the liquid or by the bottom of the liquid
container. If the weight of the object is less than the weight of
an equal volume of liquid, the object will float with a portion
of its volume not submerged, such that the submerged volume
displaces just enough liquid to support the weight of the
thing.
|
 |
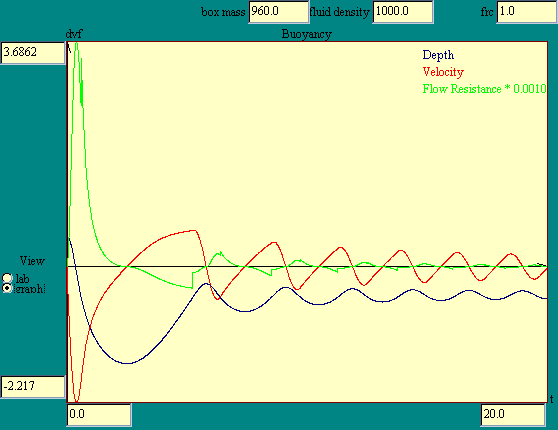 |
Run the buoyancy model to play
around with various densities of liquid and solid stuff. In the
buoyancy model we find a block of solid material held at the
surface of a pool of liquid. A click of the Action button
releases the block. As it settles into the water the buoyant
force, equal to the weight of the displaced fluid, opposes the
weight of the object. In the example given the object weight is a
bit less than weight of an equal volume of the liquid so the
object will ultimately float. Because the cube is dropped from an
elevated position with its lower surface just touching the
liquid, it initially submerges due to its downward momentum. It
takes a while for the slight positive buoyancy to turn it around.
The mass of this 1 cubic meter object is just the density in
kg/m3. By changing the mass for a fixed volume we in effect
control the object's density. Enter 500 in the box mass field and
re-run the model. You should see the sort of bobbing behavior
that a massive, somewhat buoyant object exhibits when slid into
the water.
Use the arrow keys to run the model in stop action and observe
the flow resistance vector label. Click on the drawing area to
give the keyboard focus to the model window, making the arrow
keys active.
I could not bring myself to ignore the effect of fluid
friction. Frequently we ignore air resistance for slow moving
objects but ignoring water resistance throws out a major
contributor to the motion of the object. You may remove the
effect of friction by setting the flow resistance coefficient,
frc=0. You may change the density of the fluid by entering a new
value in the fluid density field.
This model offers another view of the buoyant object's
behavior. Select the graph view for a plot of depth vs. time. By
clicking on the plotted variable labels in the top-right quadrant
of the graph, you may toggle on and off the individual plots. The
model automatically re-scales the plots to accommodate the
selected variables. Because the flow resistance is so out of
scale with the other plotted parameters, the model scales it back
by a factor of 0.001 for plotting.
|
| Next we take a brief look at fluid dynamics. Fluids in motion
relative to solid objects, like rivers flowing past rocks and
airplane wings passing through air, is a topic not yet completely
understood by anyone. Advances in chaos theory may shed some
light on exactly what is going on in these situations. Even what
is understood of the subject tends to lead us into mathematical
difficulties that are just too hard. In introductory physics
courses like this we need to introduce some major
simplifications. Even so there is a lot we can do in this area.
In this course we will consider the flow of an ideal fluid
with the following properties.
1. An ideal fluid in non-viscous. This means that internal
friction in the fluid may be neglected.
2. An ideal fluid exhibits steady flow. This means that the
velocity of the fluid at each point remains the same as time
passes. No starting and stopping transients are considered.
3. An ideal fluid is incompressible. This means that the density
is not a function of time or space.
4. An ideal fluid has zero angular momentum everywhere. This
means that the flow doesn't swirl around in eddies or
whirlpools.
Properties 2. and 4. limit the velocity of an ideal fluid to less
than the critical velocity where turbulence begins. Flow without
turbulence is called laminar flow because the fluid layers sort
of slide over one another.
The path taken by a fluid particle in an ideal fluid is a
smooth line called a streamline. The particle velocity at any
instant is tangent to this streamline. No two streamlines can
cross each other because if they did, a particle could move
either way at the crossover point and the flow would not be
steady. The entire bundle of streamlines in a flow is called the
flow tube. No fluid may enter of leave this flow tube; otherwise
the streamlines would be crossing each other. The image at the
right shows laminar flow except near trailing edge of the object
in the flow path.
|
 |
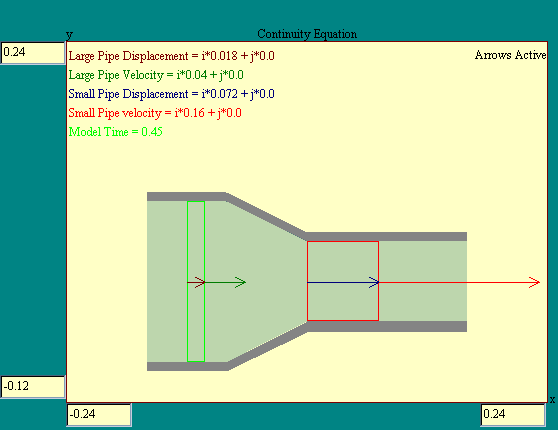 |
Now let's consider an ideal fluid flowing through a pipe with
non-uniform cross-section. We will think of the region of large
cross-section region 1 and that of smaller cross-section, region
2. The continuity equation model
illustrates the following discussion. The particles of fluid move
along the streamlines in steady flow. Imagine a surface
perpendicular to the flow in region 1. If the velocity of the
fluid flowing through this surface is v1, then in time
Dt an imaginary cylinder of fluid, of
length Dx1=v1*Dt, will pass through the surface. If
A1 is the cross-sectional area of the pipe in this
region then the volume of the imaginary cylinder is
DV1 =
A1*Dx1 =
A1*v1*Dt.
The mass of the fluid in this imaginary cylinder is
Dm1 = r*A1*v1*Dt
Now let's place another imaginary surface perpendicular to the
flow in region 2 where there is a smaller cross-sectional area,
A2. By exactly the same reasoning the mass that flows
through this surface in time Dt is
Dm2 = r*A2*v2*Dt.
Now because the mass is conserved and the fluid is
incompressible we know that
Dm1 = Dm2
and
A1*v1 = A2*v2 =
constant
This is called the continuity equation. The continuity equation
tells us that where the cross-section is small, the velocity is
large and where the cross-section is large the velocity is small.
The product of velocity and cross-sectional area is called the
volume flow rate and has units of volume/time. The constant
volume flow rate tells us that the amount of fluid put in at one
end of a pipe is the amount coming out at the other end,
regardless of the shape or length of the pipe.
|
|
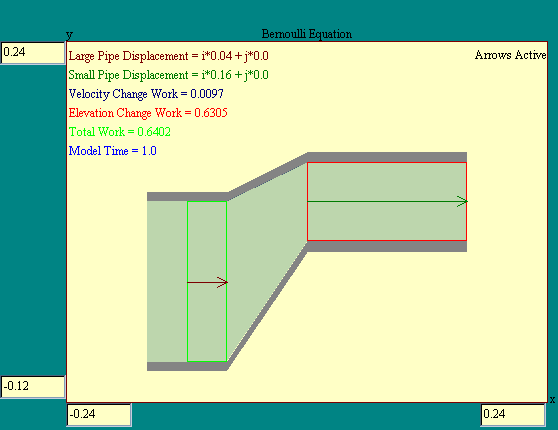
Next we will look at the work done as fluid flows through our
pipe of varying cross-section and this time we will include
variations in elevation between region 1 and region 2 as well.
The Bernoulli equation model
illustrates this situation. Consider the flow of an ideal fluid
through a non-uniform pipe in time Dt.
The force, f1, pushing fluid into region 1 of the pipe
is P1*A1 where P1 is the
pressure in region 1 of the pipe and A1 is the
cross-sectional area of that region. The work, w1,
done by this force is f1*Dx1.
w1 = P1*A1*Dx1 = P1*DV1
Likewise the work done on the fluid in region 2 of the pipe
is
w2 = -P2*DV2.
The minus sign on the work is because the force and displacement
are in opposite directions in region 2, since the fluid flows
from region 1 to region 2. The continuity equation tells us that
DV1=DV2 so the net work done,
w1+w2 is Dw =
(P1-P2)*DV
Part of this work goes into changing the kinetic energy of the
fluid and part goes into changing the gravitational potential
energy. The change in kinetic energy is
Dke = 1/2*Dm*v22 - 1/2*Dm*v12
where Dm is the mass moved through the
pipe in time Dt. The change in
potential energy is
Du = Dm*g*y2 - Dm*g*y1
where y1 and y2 are the elevations of
regions 1 and 2 respectively. The work-energy theorem says that
for this volume of fluid
Dw = Dke +
Du
or
(P1-P2)*DV =
1/2*Dm*v22 -
1/2*Dm*v12 + Dm*g*y2 - Dm*g*y1
Dividing by DV and replacing
Dm/DV by
the density r we get
P1+1/2*r*v12+r*g*y1 = P2+1/2*r*v22+r*g*y2
This last is Bernoulli's equation for an ideal fluid. It says
that the sum of the pressure, the kinetic energy per unit volume
and the potential energy per unit volume has the same value at
all points along a streamline. This is an extension on the simple
conservation of energy because it brings the pressure into the
equation. If there is no change in elevation the potential energy
terms drop out and we see that
P2=P1*v12/v22 is,
indicating that pressure is lower in the high velocity areas in a
system.
|
 |
 |
You can apply Bernoulli's equation to any number of fluid
flow problems, as you will see from your physics text. This
equation is so generally applicable that people sometimes stretch
it to cover situations where it does not really fit. One classic
is the explanation of the lift from an airplane wing. The story
goes that the curved shape of the top of the wing forces the air
passing over the top to take a longer path than the air passing
beneath the wing. Therefore the velocity of the air above must be
faster than the velocity of the air underneath; resulting in
reduced pressure above and lift from the wing. If that were the
mechanism for producing lift, inverted flight would be impossible
and the wing of a typical light aircraft wound have to have a
cross-section like this. |
|
Alternatively a four-seater Cessna 172 would have a stall
speed of 400 miles per hour with its existing wing if Bernoulli
was solely responsible for lifting the weight of the plane. The
underlying assumption is that it takes the over-wing air the same
length of time to reach the trailing edge of the wing as the
under-wing air. There is no guarantee of course that this
happens. In fact the over-wing air gets there considerably
faster.
If we think of the airplane wing in terms of Newton's third
law, the lifting force must have an equal an opposite downward
thrust. Actually the air passing over the wing has a significant
downward velocity when it leaves the trailing edge. The details
of the actual airflow are nowhere near the conditions for an
ideal fluid. We should not be surprised that Bernoulli comes up
short as an explanation. It is true that the air pressure on top
of the wing is reduced but the Bernoulli explanation is not even
close.
Are there any questions?
|
 |
  Next Next  Previous Previous  Other Other
|




