|
When what goes around comes around...
|
Imagine that a particle is subject to a force of constant
magnitude but whose direction may change. The particle's
acceleration at any instant would be in the direction of the
force at that instant. The change in the particle's velocity over
a very short time would be a vector in the direction of the
average acceleration. The new velocity at the end of this tiny
time interval would be the vector sum of the original velocity
and the change in velocity. The displacement of the particle
during the little time slice would be given by the average
velocity times the Dt. Now suppose
that the changing direction of the force was such that the force
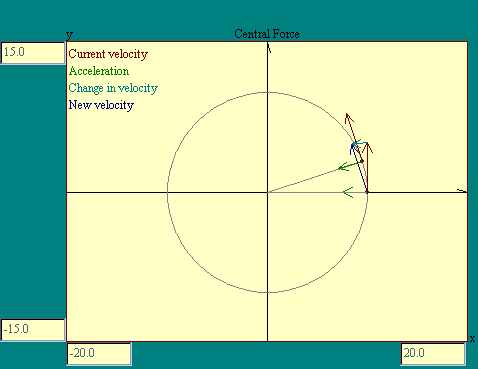
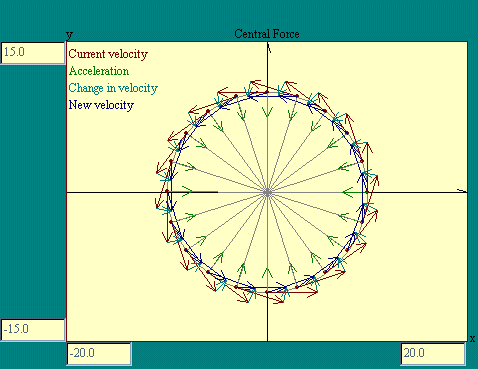
was always perpendicular to the velocity. The Central Force display illustrates this
situation.
Notice that in this example that the force bends the path of
the particle into a circle and that the force vector and
therefore the acceleration always points toward the center of
that circular path. The magnitude of the velocity along the path
remains constant. Under these conditions the particle is said to
be undergoing uniform circular motion where "uniform" means the
speed of the particle is constant. We have evidently caught this
system in a delicate balance where in each Dt the force deflects the particle just enough
from the trajectory it would have followed, a straight line in
the direction of the velocity, that it ends up on a circular
path. The question now is what must be the relationship among the
acceleration, velocity and radius of the circle for us to get
this nice result.
|
 |
 |
 Here we are going to work some tricks that you
might leave you thinking, "There is no way I would have thought
of this on my own!". What we are going to do is a typical
physicist's ploy of looking around for any relationship among the
variables in which we are interested. Then seeing if there is any
logic that leads to the relationship we want. One of the things
that make this seem like magic is that we do not show you all the
false leads and dead ends that were tried before this line of
reasoning presented itself. The other thing is, this business
gets easier with experience. Having worked out a few of these
connections helps in working out new ones.
This sort of thing, by the way, drives us mathematicians
crazy. We like things to follow absolutely one step after the
other so that we are driven inevitably to the correct solution.
This business of jumping in sort of in the middle of a problem
with some idea what the answer is going to be and using a mixture
of physics, logic, geometry and intuition to get a result that
then may be tested by experiment is really a physicist thing.
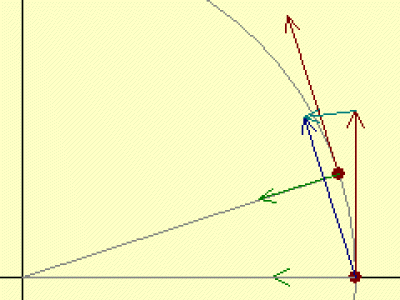
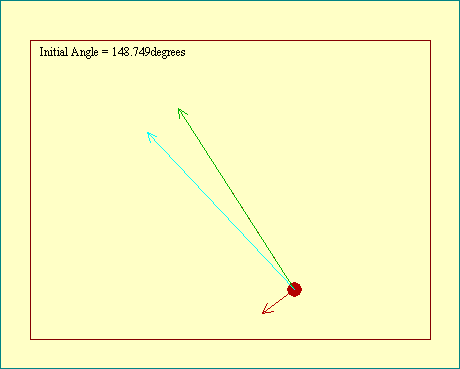
Using the image at the left, taken from the Central Force display, Take a good look at the
little red/cyan/blue triangle made up of original velocity,
change in velocity and new velocity vectors. A blue copy of the
new velocity vector was placed at the base of the original
velocity vector. Now compare that to the figure made up of the
two gray radius lines and the arc included between them. Except
for the fact that the second figure has a curved line for one
side the two are similar triangles, meaning that the angles in
the two triangles are the same. By taking Dt sufficiently small, the effect of the curvature
may be made negligible.
|
| Now the thing about similar triangles is that the ratios of
corresponding sides are equal. So the ratio of the cyan side over
the red side in the small triangle is equal to the ratio of the
arc length over the radius in the larger figure. The length of
the cyan side is the magnitude of the change in velocity,
|Dv|. The length of the red side is
the magnitude of the velocity, |v|. The length of the arc is the
magnitude of the velocity times the time increment
|v|*Dt. And the length of the gray
line is just the radius of the circle, r. So we get the following
relationship. |Dv| /
|v| = |v| * Dt / r.
We were interested in the relationship among acceleration,
velocity and radius that gave us this nice circular motion. The
magnitude of the acceleration, a|, is |Dv| / Dt so let's
divide both sides of the preceding equation by Dt. Then to get acceleration by itself on one side
of the equation, multiply both sides by |v|. These maneuvers get
us this relationship, |a| = |v|2 /
r, which ties together the acceleration, velocity and
radius as we set out to do. Any time we find a particle in
uniform circular motion it has an acceleration of magnitude
|v|2 / r with a direction always perpendicular to the
velocity. Of course being perpendicular to the velocity which is
tangent to the circle, the
acceleration vector points toward the circle's center.
|
 |
 |
An acceleration of the sort we have been talking about, one
that points toward the center of the circular motion of a
particle, is called centripetal (center seeking) acceleration.
Any particle whose direction is changing is undergoing a
centripetal acceleration of magnitude |v|2 / r where r
is the radius of
curvature of the particle's path. The direction of the
centripetal acceleration is along the radius of curvature.
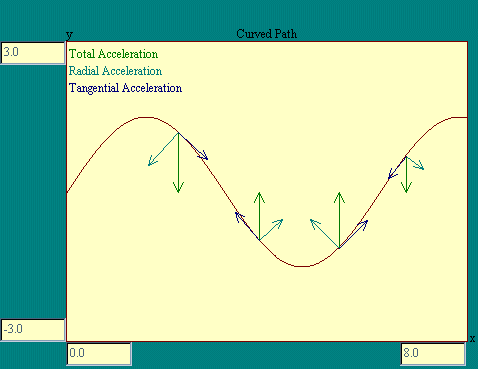
Now let's imagine a particle whose path is curved but not
circular. We know that one component of the acceleration must be
|v|2 / r in the direction of r, where r is the radius
of curvature of the path. This component of the acceleration
contributes only to the change in direction of the particle since
it is perpendicular to the path and therefore can not affect the
speed of the particle along the path. If the total acceleration
includes a component tangent to the path then the speed of the
particle is affected. The Curved Path display illustrates these
acceleration components. In the Curved
Path display you will see the path of a particle which is
moving along the x axis at constant speed and subject to a force
toward the x-axis proportional to the y displacement.
|
| Now let's go back and look at circular motion, but not
uniform circular motion. Consider a weight attached to a rod of
negligible mass which is suspended from a pivot so the rod and
weight could swing freely in the vertical plane. The Pendulum Accelerations display shows you such
an arrangement.
There is a lot to learn from this little pendulum
display. Perhaps the first lesson is that the physics of everyday
objects like a pendulum can get pretty messy, and we haven't even
got to the friction part of the story yet. The second lesson is
that we must pay careful attention to what we are really seeing.
Because of the path and speed of the pendulum weight, we know
that the radial and tangential components of its acceleration are
as displayed. If they were any different the weight would have
some other motion. What this display does not show you is the
actual forces which result in these net accelerations.
The only forces acting on the pendulum weight are gravity and the
force applied by the rod. Somehow these must always add up to the
total acceleration times the mass of the pendulum weight, in
accordance with Newton's second law.
Near the bottom of the swing, the tension in the rod must be
sufficient to both support the weight and curve its path into a
circle when it is moving its fastest. Near the 180 degree
position, the rod will actually go into compression, supporting
the weight when its speed is near zero. You will encounter many
interesting problems based on a pendulum like this. For example,
what would have to be the speed of the pendulum at the top of its
loop for the force exerted by the rod to be zero? Try to work
this one out based on what you now understand.
In the next lesson in this course we will introduce the ideas
of work and energy.
Are there any questions?
|
 |
  Next Previous Other
|
