we set the initial x to 10m, initial y to 5.77m, initial velocity to zero and let time zero be the instant that static friction bonds are broken. Suppose the coefficient of kinetic friction is 0.25. Then the frictional force will be 0.25*n where n is the normal force of the plane on the box which is cos(30)*8.9N = .866*8.9 = 8.5N. This makes the magnitude of the frictional force 2.12N. Its direction will be up the plane at 30 degrees. Set this situation up on the free body diagram and find the time for the box to reach the origin and its speed at that moment.
you should have found that the time was about 2.86s and the speed about 7.97m/s. This compares to 2.17s and 10.58m/s in the no friction case.
 Now we are going to try something foolish just so you can see what can happen. Suppose our inclined plane is real rough such that
Now we are going to try something foolish just so you can see what can happen. Suppose our inclined plane is real rough such that 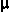 k is 0.75 instead of 0.25. That would lead us to use a friction force vector of .75*8.487 at 30 degrees. Go ahead and change the friction force on the free body diagram above to 6.28 at 30 degrees. Because I know how this is going to come out, let me tell you to set the initial position back to the origin at (ix=0 and iy=0). Then run the model by clicking on the Plot button.
k is 0.75 instead of 0.25. That would lead us to use a friction force vector of .75*8.487 at 30 degrees. Go ahead and change the friction force on the free body diagram above to 6.28 at 30 degrees. Because I know how this is going to come out, let me tell you to set the initial position back to the origin at (ix=0 and iy=0). Then run the model by clicking on the Plot button.
As you can see the model we are using predicts that when the 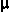 k is 0.75 the box takes off and goes up the plane. There are a few lessons to be taken from this. First is that we have to check that the results of our model does not violate common sense, which happens in this instance. If what we see is contrary to common sense, the first thing to check is the whether we did bad physics in setting up the forces. That is what happened here. The friction force can never exceed the force which produces the motion, in this case the force vector down the plane which is 9.8N * sin(30) or 4.9N. Also check that the constraints of the model have not been violated, for example by including some non-constant forces.
k is 0.75 the box takes off and goes up the plane. There are a few lessons to be taken from this. First is that we have to check that the results of our model does not violate common sense, which happens in this instance. If what we see is contrary to common sense, the first thing to check is the whether we did bad physics in setting up the forces. That is what happened here. The friction force can never exceed the force which produces the motion, in this case the force vector down the plane which is 9.8N * sin(30) or 4.9N. Also check that the constraints of the model have not been violated, for example by including some non-constant forces.
 Now we are going to try something foolish just so you can see what can happen. Suppose our inclined plane is real rough such that
Now we are going to try something foolish just so you can see what can happen. Suppose our inclined plane is real rough such that 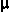 k is 0.75 instead of 0.25. That would lead us to use a friction force vector of .75*8.487 at 30 degrees. Go ahead and change the friction force on the free body diagram above to 6.28 at 30 degrees. Because I know how this is going to come out, let me tell you to set the initial position back to the origin at (ix=0 and iy=0). Then run the model by clicking on the Plot button.
k is 0.75 instead of 0.25. That would lead us to use a friction force vector of .75*8.487 at 30 degrees. Go ahead and change the friction force on the free body diagram above to 6.28 at 30 degrees. Because I know how this is going to come out, let me tell you to set the initial position back to the origin at (ix=0 and iy=0). Then run the model by clicking on the Plot button.