In the previous section we worked with a pendulum and found that the actual behavior was only approximated by the simple equation, p=A*sin(t) . In fact the actual solution to the pendulum differential equations has infinitely many terms in it. That is because the force tending to restore the pendulum to the equilibrium point is non-linear. Gravity pulls straight down and the pendulum bob swings in an arc so the restoring force is weight times the sine of the displacement angle. The sine function of course is non-linear.

Now we will examine Mr. Duffing's oscillator. An "oscillator" by the way is anything which moves but remains in a our vicinity. All the dynamical systems we will discuss are oscillatory in nature. Think about it. If they were not, the moving parts would just disappear over the horizon, never to be seen again, and so the system would not be of much interest to us. Remember we are in the future predicting business and once something is gone out of our observation and will not be back, even if it has fantastic adventures, we will not know it.

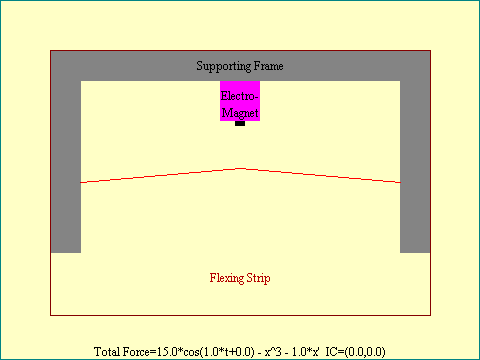
This apparatus was explored by a person named Duffing back in 1918 so we call it Duffing's mechanical oscillator (DMO). It consists of a light metal bar, hardly more than a thin strip, attached at each end to a solid support. Near the middle of the metal bar is an electro-magnet powered by alternating current. As the current in the magnet goes through a cycle, the magnetic field couples energy into the bar, causing it to move. The movement is a flexing of the bar. Run the Duffing's Oscillator, Real Space view display for an illustration.

As the bar in the oscillator flexes, the position of the midpoint may be used to measure the amount of movement. Since the bar is tightly suspended between supports that may be considered immovable, any transverse displacement of the bar must stretch the bar material. Metal is not easily stretched so there is a strong force tending to snap the bar back from any displacement. This force is proportional the displacement cubed. Energy is lost each cycle to air resistance and internal heating of the bar. Energy is added by the electromagnet, exerting force on the bar.

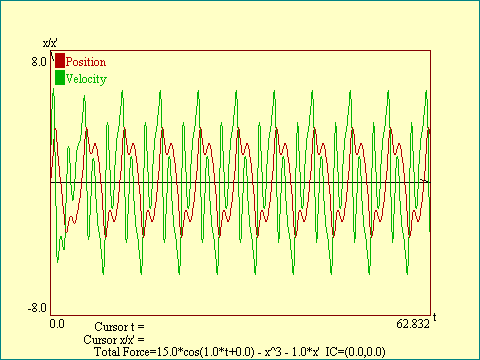
The frequency of the current energizing the magnet is taken to be fixed for the time being. The "amplitude" or strength of the magnetic field is one of the control parameters of the system which can be varied. The other system parameter we control is the rate of energy loss. We call this parameter the "energy loss coefficient" or "drag". In addition to the system variables of amplitude and drag, we may vary the initial value of position and velocity. These values relate to the particular experiment rather than to the system itself. Run the Duffing's Oscillator, Position/Velocity vs. Time View display.

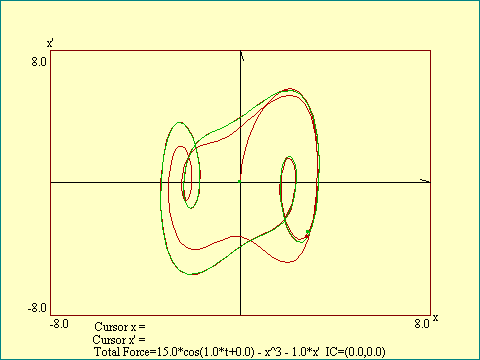
Remember that we examined the motion of the pendulum in phase space, a space spanned by position and velocity. In the driven pendulum case, the motion settled out on an attractor that would be nearly elliptical in the phase space projection view if the energy loss and gain per cycle were small. The DMO under the conditions established for the Duffing's Oscillator, Phase Space Projection View also settles to a limit cycle consisting of one orbit per cycle period. Its shape is more complex than the simple ellipse of the pendulum.

Notice that the initial conditions, at the origin, lie quite a way from the attractor so that it takes somewhat more than a cycle form the electromagnet before the oscillator finds the attractor. The color change after this startup transient dies away marks the actual attractor.

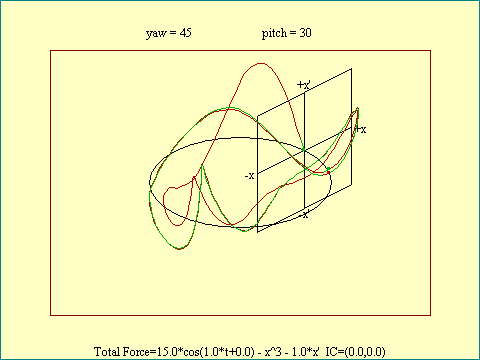
In the case of the pendulum phase space orbit, including the time dimension, where the orbit cycle time was adjusted to match the pendulum period, we found a fairly simple curve representing the attractor for the pendulum. The corresponding attractor for the DMO is quite a mess in 3D phase space. Run the DMO, Phase Space Orbit View to see it. As with the phase space projection view, the image shown here includes a color change to highlight the actual attractor.

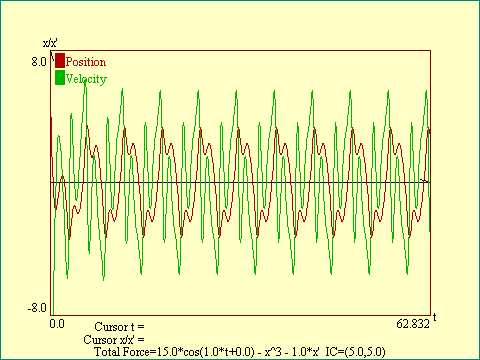
Enough about the innovations of the Duffing Oscillator display, let's get back to the thread of the story. Looking at the Position/Velocity vs. Time view, notice how jagged the plot is. The motion of the strip is evidently more complicated than the pendulum. The motion is still periodic though. It repeats with some definite period. It may be difficult in this view to determine that the plot does not show subtle difference between states in successive cycles. As we will see later, patterns that look somewhat like this actually never repeat. Compare this time series plot to the one above. Notice that they differ in the first few cycles but after that are similar.

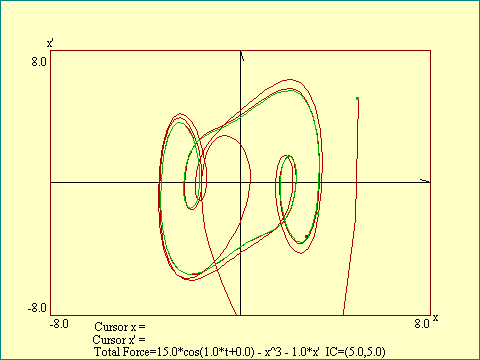
To confirm that we have periodic motion here, look at the Phase Space Projection view view. After the startup transient the projected orbit is quite stable. Notice that we started the DMO for different initial conditions than in the previous models but that the attractor is the same. That is the nature of an attractor, it gathers up motion started from many different initial conditions. Many but not all, as we will see.

Also notice that at one point on the orbit of the states in phase space there is a differently colored marker. This marks the chronon at which the forcing function returns to its initial value or one cycle time. This is called the return point and since only one return point is marked, we know that the motion completes its cycle in the same time that the forcing function completes its, so we have a "period 1" kind of motion. We will see examples of other periodicity later.

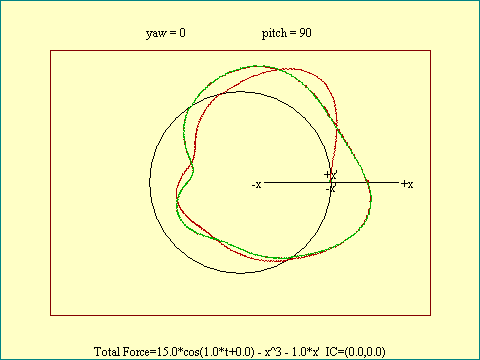
The Phase Space Orbit view of this dynamical system again reveals that there is only one loop per cycle of the forcing function. Granted it is a warped looking affair, but still it only completes one circuit of the time axis each cycle. To verify this pitch up to 90 degrees so the variations in velocity do not complicate the picture. Notice that this view also marks the return chronon in the distinctive color.

Are there any questions?