In iterating a single transform, even one that included shrink, spin and displacement components, the trajectory of points on the screen was predetermined. A single transform always moves a certain point in a certain way so that most of the screen is inaccessible from any given point. Now we want to consider the situation where there are two or more transforms available, and we can choose which one we will apply at any time. The transforms we will use for now are:
1. xsize=1 , ysize=1 , xspin=PI/4, yspin=PI/4,xdisp=0, ydisp=0
2. xsize=.9, ysize=.9, xspin=0, yspin=0, xdisp=1,ydisp=0
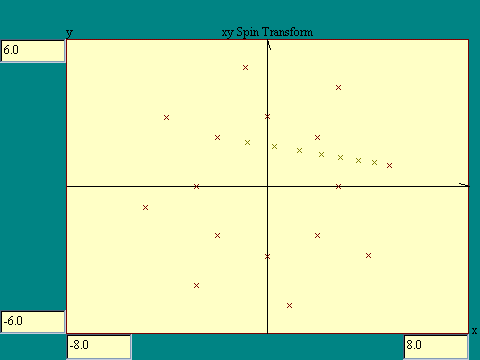
Run the selectable transform display. Notice that in the image at the right from that display, there are two octagonal arrays of marks connected by a straight line. This shows that a spin transform was iterated 8 times followed by 8 iterations of the shrunken displacement transform and then 8 iterations of the spin transform again.

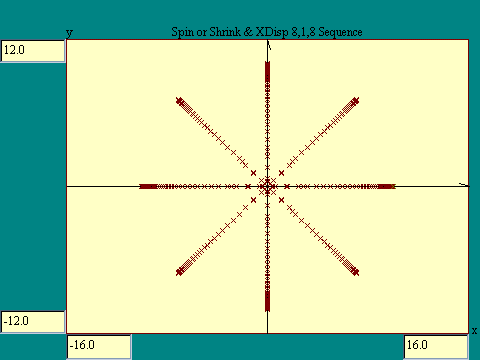
Remember that with each change of transform, the starting point for the iteration of the new transform is the last point landed on by the old transform. Run the 8-1-8 transform pair display. In this display we run 8 iterations of the xy spin transform followed by a single iteration of the xy shrink and displacement transform. As this process repeats we create a collection of octagonal arrays of points of different diameters.

As you can imagine, there are a great many possible sequences in which these two transforms might be called. Consider what sort of pattern might be developed by invoking these transforms in a different order. If we run the xy spin transform 9 times to every 1 of the xy shrink and displacement transform, each radial move will start from the spin location one iteration father along than the previous.

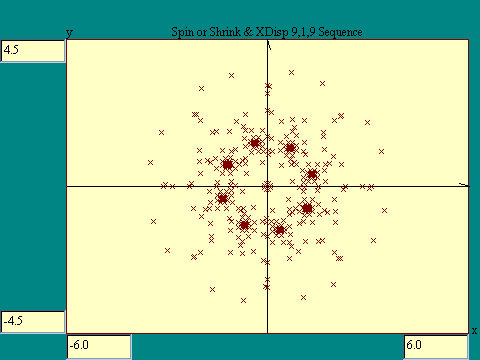
To illustrate that situation, run the 9-1-9 selectable transform display. You will notice that the ultimate patterns that developed on the screen are quite different from the 8-1-8 case even though the transforms are identical.

The point of the last two displays was to illustrate that by mixing the application of two affine transforms, complicated patterns of points might be produced and the nature of those patterns depends on the order in which the transforms are applied. The sequence in which we applied the two transforms had in each case a definite order to it. If we had sufficient time and patience to try all possible combinations of our two transforms, we would discover that there would still be some areas of the screen that were not accessible. Like the directions to East Millinocket, you can't get there from here.

The set of all points that can be reached using a given set of transforms comprise an interesting figure that is finite in extent but has an infinite boundary. This of course is the fractal that we promised to generate in this section. As a practical matter, it takes too long to lay out and carry out a scheme to cover all possible sequences of calling even two transforms. With more than two it is worse. The best we can do is to approximate the full range of possibilities by selecting the transforms in a nearly random fashion and let the process run for a long time.

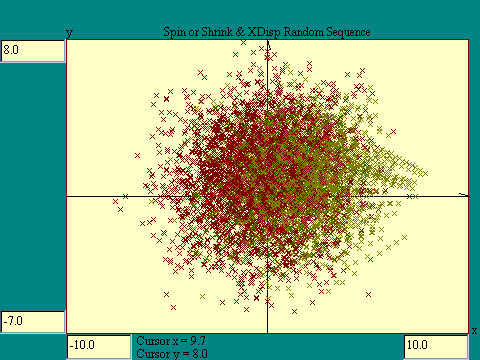
To illustrate this technique, run the Spin or Shrink + X Displacement - Random display. What you will see is not particularly impressive, sort of a non-descript blob, indicating that the choice of the example transforms was not well thought out. This serves to illustrate that not all affine transform combinations yield interesting results.

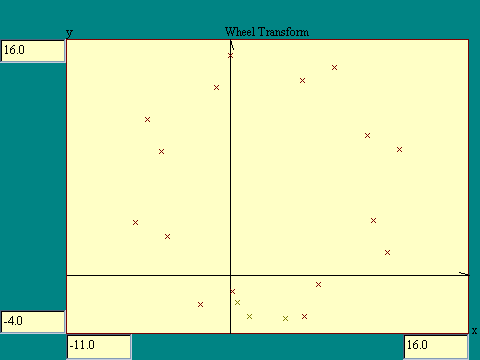
Consider next a pair of transforms we will call the pinwheel pair.
1. xsize=1, ysize=1, xspin=PI/4, yspin=PI/4, xdisp=5, ydisp=0
2. xsize=.5, ysize=.5, xspin=-PI/4, yspin=0, xdisp=0, ydisp=0
Notice that transform 1 spins the point 45 degrees counterclockwise and shifts it 5 units in the +x direction. The number 2 transform shrinks the point toward the origin and spins the x component of the point 45 degrees clockwise. Run the pinwheel pair transform display to see these transforms in action.

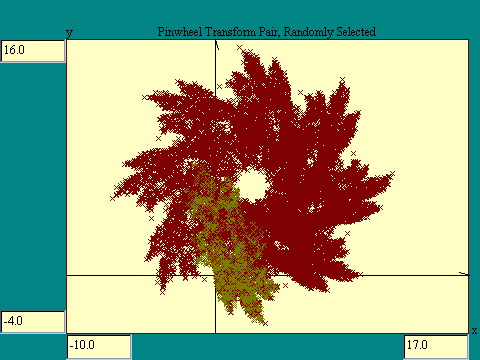
Now to see the sort of image which may be generated by random application of this transform pair, run the random pinwheel pair transform display.

There is nothing necessary about the randomizing process. You could have achieved the same results by systematically exploring all the possibilities with manual transform selection. The total picture is defined by the two transforms as they operate on one another. Each one provides a source of starting points for itself and the other. The randomizing process just makes it easier to cover the many possibilities than does the manual process. Also the transform selection process is not strictly random. Random selection would mean that each transform would have an equal opportunity at being selected. Some transforms however cover more area than others. So as to optimize the process, "big" transforms are favored in the selection algorithm.

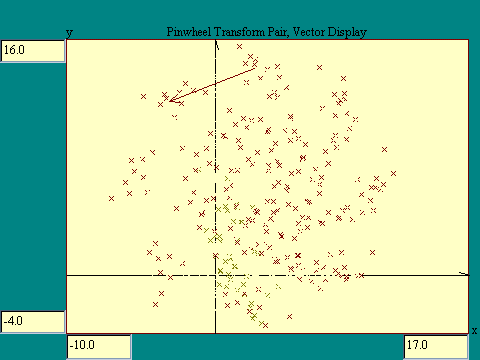
There is an alternative way to display the effect of the transforms as they are randomly iterated. That is to show the transformed point as a vector. In the next display we do that, Color-coding the vectors red for transform 1 and yellow for transform 2. This is intended to help you visualize how each transform takes its starting point to a new location. In order for a point to be lit, it must satisfy the condition that it may be reached by one of the two transforms from a point that has already been lit under the same restriction. Run the transform vector display.

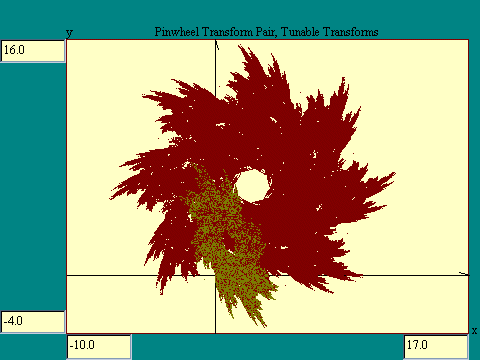
The iterative process by which points are lit on the screen leads to the development of a complex picture as the two transforms exchange information. In the next display we do away with some of the artifacts that we attached to our points previously like x'es and vectors, and just light the corresponding pixel. Notice that we start the process with x=-4 and y=-2 and that a few of the initial points are not connected. These two transforms define a figure that does not extend that far out, farther illustrating the point that only a limited set of points is accessible to this pair of transforms. Also pay attention to the boundary of the figure. It looks like a fractal boundary and so it is. Run the Tunable Transform display.

In the image at the right I let the display run for a long time. Notice that there are holes on the left half of the image that are larger than those symmetrically placed on the left. Think back to the lesson on extending graphing concepts where we used random chance to fill in a graph. This is an extreme example of the same idea. In sufficient time perhaps most of the interior holes would get filled in. I suspect that the central hole though is permanent.

In the Fractal Generation Research display we start you out with a four transform example. You may modify the transforms and add up to two more. You may select any number of up to six transforms to be active. The zoom feature, introduced in earlier lessons, is enabled in this display. The limitations of the Java language and web security prevent us from offering you the opportunity to save your work and reload it at a later time. The Windows version of "Order - A closer look at chaos" has that capability and more that we cannot duplicate on the web.

You will find with a little practice you can create some striking images by experimenting with the Transform Control Panel. This program is intended only to provide a rudimentary capability in this area as an aid to understanding the mathematics behind the process. Serious image production requires the use of a dedicated fractal graphics program.

Are there any questions?