There is only one Mandelbrot set and every number in the complex plane is either in or out of the set. Associated with every point in the complex plane is a set somewhat similar to the Mandelbrot set called a "Julia" set after the mathematician Gaston Julia. In developing the Mandelbrot set we examined points in the complex plane to see if z²+c diverged or not. Remember that in this function c represents the coordinates of the pixel location being examined. When we shift to a different point we use that point's coordinates in the function as c. Click on the label above each image to see the set boundary illuminated.

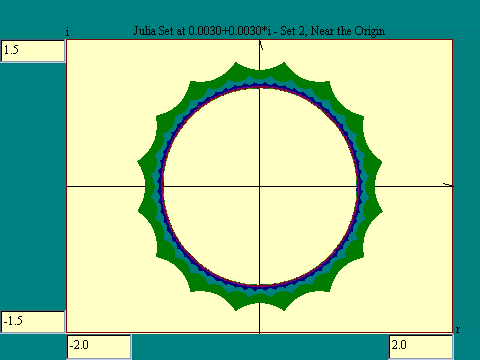
If we examine points in the complex plane to see if z²+k diverges, where k is a fixed complex number, we get the Julia set associated with the point k. Instead of changing the constant in the function as we move from pixel to pixel, we hold the value of k fixed as we scan the screen. Julia sets and the Mandelbrot set are close relatives. The Julia set boundary will be illuminated by the escape time algorithm as was the case for the Mandelbrot set. Julia sets take several different forms depending on the location in the plane of the fixed point k.

The set boundaries illustrated on this page amount to a guided tour of some of the possibilities. The first five images show an entire Julia set boundary. Note the coordinates of the fixed point in the label above the drawing area. Each Julia set is contained in the same region of the complex plane as is the Mandelbrot set. In fact the Mandelbrot set has been called a catalog of the Julia sets. Many similar structures are seen in both sets. The boundaries of either might be considered the ultimate fractal object.

Next we will pick a particular Julia set and zoom in on it as we did the Mandelbrot set. You will see that at higher magnifications the similarity between Julia and Mandelbrot increases. If we jumped from one to the other at high magnification you would have trouble telling them apart. In the research display you will be able to proceed from the Mandelbrot set at high magnification to the corresponding Julia set. Keep in mind that the instructions for all this detail is contained in a few lines of computer code. Run this group of Julia Set displays.

Next you may explore the Julia sets by marking points on the screen and using the Action button to generate the corresponding Julia set. You will find that there are several types of Julia sets depending on where the reference point is located. Run the Exploring the Julia Sets display.

In the next display you will be able to select points for the Julia set with the Mandelbrot set outline on the screen. Run the Mandelbrot Set/Julia Sets Relationship display.

The next display in this section allows considerable flexibility in exploring the Mandelbrot and Julia sets. Run the Complex Sets Research display.

Are there any questions?