|
|
|
|
This is not simple...

|
In this section we will extend iteration into an additional dimension. The image at the left
is created based on the way a certain function approaches its attractor under iteration. It
is a small segment of the boundary of an object called the Mandelbrot set. In the interest
of full disclosure, I must confess that the image was created with the offline version of the
Order program,
in which we have better control over the colors and shading. The online Java applets serve
to illustrate the concepts, but lack the power of the compiled native code Windows
version.
The Mandelbrot set and related Julia sets are prime examples of the complexity hidden in
simple systems. The mathematics behind these objects is straightforward. The results are
fantastically detailed and beautiful. Before we get into the details we need to lay some
groundwork.
|
|
We will briefly review the concept of a "real number
line" which we covered in
Numbers Functions and Graphs.
We have made use of
this sort of number line in laying out the axes of the graphs
displayed so far. This line of numbers is generally taken to be
increasing to the right or up, extending from minus infinity to
plus infinity. The number line is "everywhere dense"
meaning that between any two numbers however close, there are
infinitely many other numbers. Included on the real number line
are integers, fractions and irrational numbers.
The image at the right illustrates a
short segment of the real number line, between -20 and +20. The
indicated example here is an irrational number. Click on the link for the
Real Number Line
interactive display from which this example was taken.
The real numbers with which we have been working satisfy most
of the needs for calculation and accounting in our everyday life.
There is no place on the real number line however for a number
which when multiplied by itself gives a negative result, for
example the square root of minus 1. Not wishing to leave negative
numbers without square roots, mathematicians reasoned that such
roots must be off the real number line. Such numbers are called
"imaginary" numbers. They are of course as real as any
other but imaginary remains the way in which we refer to
them.
Imaginary numbers are measured by their distance from the real
number line. Like real numbers they form a whole continuum from
negative to positive infinity, an imaginary number line
perpendicular to the real number line. The lines intersect at
zero which is their only common value. The two perpendicular
number lines define a plane, a two dimensional surface, and the
question comes up, "What is the nature of numbers which do
not lie on either of the number lines?". These numbers are
called "complex". Complex numbers have a real part and
an imaginary part.
|
|
|
Complex numbers may be written as a + b times i, where a and b
are real numbers and i represents the square root of minus 1.
This formula means go a distance a along the real line, turn 90
degrees left and go a distance b in the imaginary direction.
Multiplying by i has the effect of redirecting movement in the
complex plane 90 degrees counterclockwise. All numbers may be
thought of as complex numbers of the form described. If b happens
to be zero, the number is all real. If a happens to be zero the
number is all imaginary.
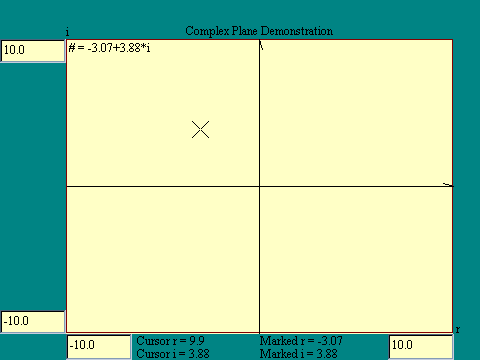
The Complex Plane display shows a region of the complex plane,
bounded by upper and lower limits in both the real and imaginary
dimensions. Real values are plotted horizontally and imaginary
values are plotted vertically. What was the x-axis in previous
displays is now the r (real) axis. The former y-axis is now the i
(imaginary) axis. The limiting values are displayed in input
boxes located near the ends of the left and bottom boundaries of
the displayed region of the complex plane. If limit changes are
appropriate, you may enter new values in these input boxes.
There is a series of control buttons across the top of the
display. When required, the Action button causes the display to
do something. If the action is continuous, the Cut button is
enabled so you can turn the action off. The remaining buttons
allow you to manipulate the size and location of the displayed
region of the complex plane if that is appropriate. The Near
button reduces the limits symmetrically by 25%, effectively
bringing any plotted objects nearer to the viewer. The Far button
has the opposite effect. The Left, Right, Up and Down buttons
shift the visible region of the complex plane one whole window in
the indicated direction. Buttons that are not required for a
particular display are disabled.
Run the
Complex Plane
display and experiment with the controls.
|
|
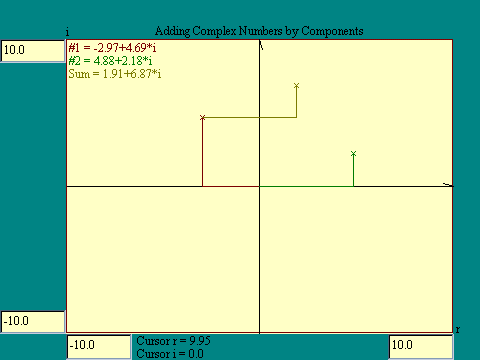
The ordinary arithmetic
operations of adding, subtracting, multiplying and dividing are
defined for complex numbers. We will be dealing with addition and
multiplication in this section of the program. To add complex
numbers just add the real parts together and the imaginary parts
together to form the sum. Plotting the numbers on the complex
plane illustrates the process. Run the
Complex Number Addition
display.
|
|
|
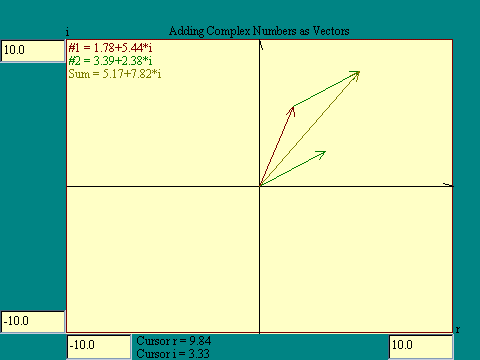
An alternative way to represent a complex number in the plane is to show it as a
directed line segment. A line of a certain length in a given
direction. This sort of line segment is called a
"vector". Each complex number may be thought of as a
vector from the origin (0+0*i) to the number (a+b*i). With regard
to vectors we speak of a head and a tail. The head of a vector is
located where the line ends, the tail where the line begins. We
put an arrowhead on the head end of the vectors. To add complex
numbers then we may just place them tail to head. The sum is a
vector from the origin to the head of the added vector. Run the
Complex Number Vector Addition
display to see this.
|
|
The previous displays illustrated the adding of complex numbers
which is a straightforward process intuitively similar to the
adding of real numbers. Multiplication of complex numbers is more
complicated and does not have such a simple geometric
representation in the complex plane. To multiply two complex
numbers we must multiply them as binomials. This means that we
multiply each part of one number by each part of the other and
add all the products. In symbols:
(a+b*i)*(c+d*i) =
(a*c)+(a*d*i)+(b*i*c)+(b*i*d*i) .
This mess may be simplified.
In the expression:
(a+b*i)*(c+d*i) =
(a*c)+(a*d*i)+(b*i*c)+(b*i*d*i)
Consider the term (b*i*d*i). The symbol 'i' represents
the square root of -1. So i*i is just -1. This line of reasoning
reduces (b*i*d*i) to (-b*d). Now let's collect the real parts
together (a*c-b*d) and the imaginary parts (a*d+b*c)*i giving us
the complex number in the standard form as below:
(a*c-b*d)+(a*d+b*c)*i
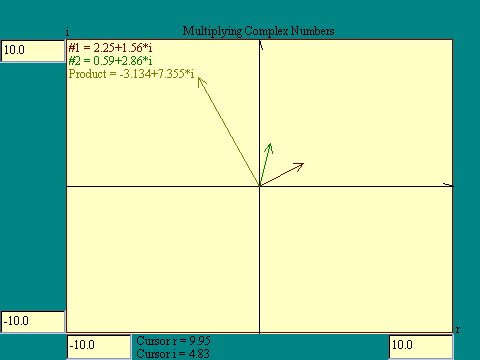
Multiplying two complex numbers then gives a new complex number as shown.
On the next display we see a graphical example of complex
number multiplication using the vector representation. The
resulting vector is not as clearly related to the two original
vectors, as was the case in addition. Run the
Complex Number Multiplication
display. You will find that the product vector has length equal to the product of the lengths of the other vectors and the angle is the sum of the other vector's angles.
|
|
|
Now that we know how to multiply complex numbers we can raise
complex numbers to a power by multiplying it by itself the
indicated number of times. For now let's just look at
squaring the number a+b*i. Based on the rule we demonstrated
above, that would be:
(a+b*i)*(a+b*i) = (a*a-b*b)+(a*b+b*a)*i
This simplifies to:
(a+b*i)2 =
(a2-b2)+(2*a*b)*i .
With the arithmetic of complex numbers under our belts, can
functions of complex numbers be far behind?
In answer to the question of the above paragraph, of course
not. let's consider the function z2=z12+c, where
z2, z1 and c are all complex numbers. This says to get z2 take
the complex number z1 and square it, then add the constant
complex number c. Given what we now know, these are certainly
do-able instructions. Next suppose that we iterate this function,
watching what happens to the value z2 as iterations occur.
Remember that iteration means we take the result z2 and plug it
back in the function as a new z1. Then calculate a new z2.
Previously when we iterated a function we were interested in
whether the result settled down to a single value, a series of
values or never settled at all except to stay in a certain range.
We will be interested in the same questions with regard to
iterating z2+c. Within the limited domain in which we
iterated the functions of real numbers, we always arrived at one
of the conditions listed. In this case, iterating
z2+c, we will find another possibility. That is that
the result of iteration may grow larger and larger without
limit.
If the sequence of numbers generated by iteration increases
without limit as suggested above, the sequence is said to
"diverge". If the sequence approaches a single finite
value it is said to "converge". As we have seen it is
possible that a function being iterated may do neither. It may
visit a set of points or it may dither about in a confused
fashion in some vicinity. In this section we will be concerned
with whether or not z2+c diverges under iteration. For
a sequence of complex numbers to diverge it is only necessary
that either part, real or imaginary, diverge.
|
|
It is likely that the result
of our iteration will depend on where we choose to begin. Think
about the real number iteration of x2. If x starts
less than 1 the function is attracted to 0 under iteration. If x
starts greater than 1, the function grows without limit. In the
next display you will have an opportunity to experiment with
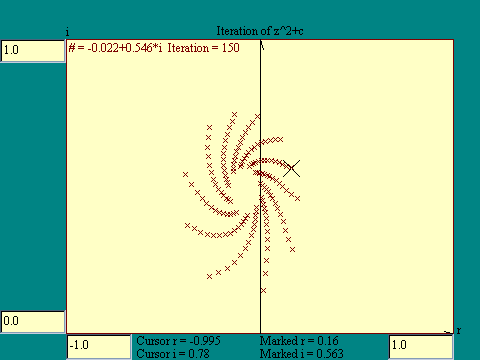
iteration of z2+c. Move the cursor to any point on the
display. This establishes the complex constant c. The initial
value of z is zero. Click on the Action button to start
iterating. Each subsequent click iterates one time.
If the absolute value of either the real or imaginary part of
z exceeds 2.0, the function is on its way to infinity and the
process is halted by killing the Action button. After the
iteration settles down, or blows up as the case may be, you may
move the cursor to another location and begin again, testing that
location for the behavior of z2+c under iteration. A
colored 'x' marks the location on the screen of each
calculated z. A trail of x's marks the progress of each
iteration. The current value of the complex number z and the
current iteration number are shown at the top left corner of the
drawing area. Run the
Iteration of z2+c
display.
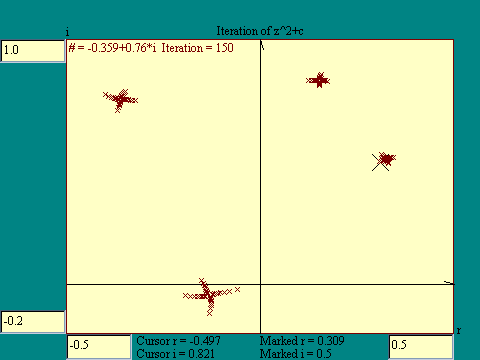
We intentionally left you without much direction on where to
try iterating z2+c on the last display. You should
have discovered that the iteration of this simple function led to
some complex results. There it is again, that theme of complexity
out of simplicity.
On the real number line, a function takes a number and
transforms it to another point on the line. In the complex plane
a function transforms a number to another point on the plane. On
the real number line, if a function approached some number as a
limit, the wildest it could get was to jump back and forth across
the limit as it zeroed in. In the complex plane there are all
sorts of paths by which a function might approach a limit. Some
of these you should have seen on the screen as a trail of colored
x's. Also you should have found that some points iterate out
of bounds.
Are there any questions?
|
|

 Next Next
 Previous
Previous
 Other
Other
|
|
|
|




