|
Affinity is a fine thing...
|
In the section on complex sets we introduced the complex plane
and observed that a complex number could be represented by a
point in the plane. The complex number z could be expressed as a
pair of real numbers, a and b such that z=a+b*i. We also
expressed points in the plane as vectors. A vector which we
pictured as a line in a certain direction of a certain length
could as well be just the two numbers written in a fixed
arrangement called a "matrix". A matrix is an array
into which numbers may be placed as illustrated below.
- | |
- | |
The vertical bars demark the places for the numbers . The matrix
representation of the complex number z would be just:
- |a|
- |b|
in this scheme.
Again thinking back to the previous section, we used the rules
of complex arithmetic to write functions of complex numbers as
for example the function z1=z0^2+z0 which generated the
Mandelbrot set. If x and y are a pair of real numbers, the
Mandelbrot function gives us a prescription for finding new x and
y in terms of old x and y. It goes like this:
new x = x^2+y^2+x and new y =
-2*x*y+y . The new x and y define a new point in the plane
so our prescription transformed the original point.
We have seen how repeatedly applying the Mandelbrot function
to itself (iterating) generates a series of points in the complex
plane. Whether that series diverged or not determined if the
starting point was in the Mandelbrot set. Each application of the
function moved the point to a new location or transformed it. So
we refer to a rule for generating a new x and y as a transform.
There are practically a limitless number of transforms that we
might make up, any relationship where new x and new y are some
function of the old x and old y would serve.
In the first display of this section
we will look at the Mandelbrot transform. In previous iterations,
we dealt with only one point at a time and tracked how that point
was transformed as we iterated new x =
x^2+y^2+x and new y = -2*x*y+y .
Here we will carry out the transform simultaneously on the four
corners of a square. We already know that how a point is
transformed by the Mandelbrot transform depends very much on
where it was located in the plane. We might expect that running
the same transform on different points would produce noticeably
different results.
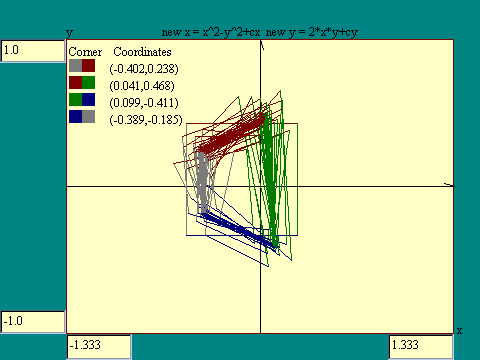
The display we will use in this section represents a portion
of a plane with dimensions x and y. The coordinates of the
corners of the square are displayed and each side of the square
is in a different color to help you keep track of the effect of
the transform. Each corner is identified by the pair of colors of
the lines that make up the corner. For example there will be a
red/green corner, a green/blue corner, etc. Clicking on the
Action button will carry out the indicated transformation in the
next few displays. Run the Mandelbrot
Transform on a Square display.
|
|
|
There is a class of transforms which is not so hard on the
figures they transform. They preserve the basic form of an object
and only rotate, stretch or move it. There is a structural
affinity of the new shape for the old. These transforms are
called "affine" transforms, reflecting that affinity.
Affine transforms do not involve raising x or y to powers or
multiplying them together.
If a plane figure is to retain its structure then it may only
be rotated, resized or moved. Each of these operations may take
place along either of two dimensions so an affine transform must
be completely defined by six numbers that we will call xsize,
ysize, xspin, yspin, xdisplacement (xdisp) and ydisplacement
(ydisp). The spin numbers represent angles, the size numbers are
scale factors and the displacements are movements. We already
know how to move points by just adding xdisp to the x components
and ydisp to the y components of the points to be moved.
The application of rotation and
resizing to points in a plane is conveniently handled by creating
a 2 by 2 matrix that contains the rotation and resizing
intelligence, then using the rules of linear algebra to multiply
the matrix times the vector representing the point to be
transformed. Following this process gets us to the point where we
have a prescription for new x and new y as we did for the
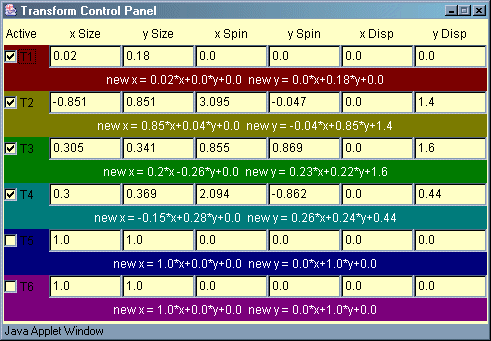
Mandelbrot transform. Affine transforms have the form: new x = a*x + b*y +e and new y
= c*x + d*y + f .
The a, b, c, and d numbers in the expressions above take care
of the rotation and resizing of points in a plane. They are
related to the spin and size numbers through the trigonometric
functions, sine and cosine as follows:
- a=xsize*cos(xspin)
- b=-ysize*sin(yspin)
- c=xsize*sin(xspin)
- d=ysize*cos(yspin)
The numbers e and f are just the xdisp and ydisp.
|
|
Now we will look at some particular affine transforms. On the
next display we will again transform a small square as we did in
applying the Mandelbrot transform. The first example has no spin
and no displacement. The resizing factors in both the x and y
dimension are 1, implying no resizing. This is sort of a null
transform, not very interesting except as a starting point. Run
the Null Transform display.
You will have noticed that acting on our square with the null
transform had no effect. Each iteration left all the corners
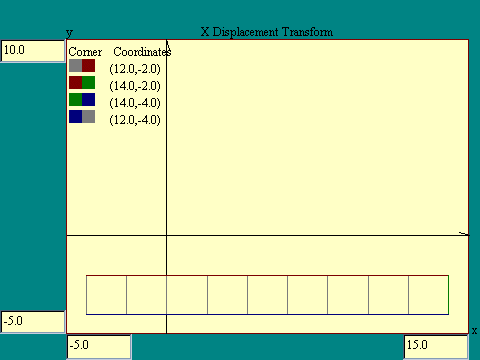
where they were. In the next display we have altered the null
transform only by introducing an xdisp of 2, the width of the
square. Run the X Displacement Transform
display.
|
|
|
If the xsize or ysize numbers were greater than 1 we would see
the squares getting larger and farther from the origin. Iterating
such a transform would quickly run us out of bounds. Since we are
not going to be interested in transforms which diverge under
iteration, we will restrict ourselves to size parameters less
than or equal to 1.
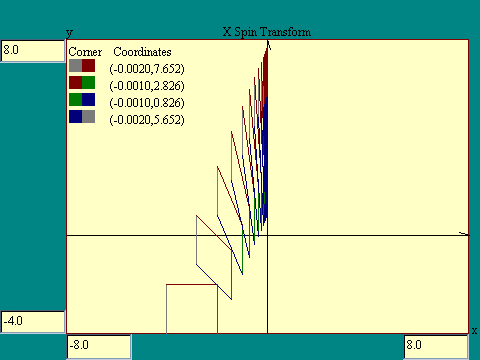
Next we will examine the effect of xspin on the square. Run the
X Spin (swing) Transform display.
|
|
|
Now we will look at the effect of yspin by itself. It is
completely analogous to the xspin case but rotates vertical
components. In a later display you will be able to vary the
transform values. Try repeating these transform with xspin or
yspin as the only non-null item. By experimenting with different
spin values you will develop some feel for what these terms in
the transform do. It is much easier to observe experimentally
than to calculate or intuitively predict the result of the spin
terms by themselves. Spin with additional terms is even harder to
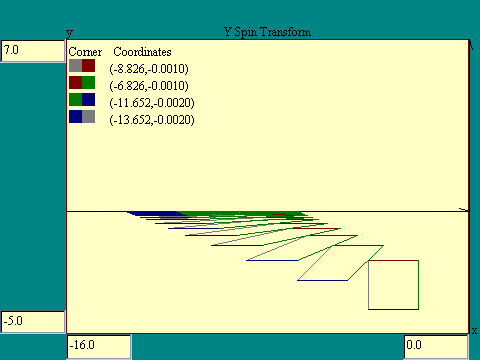
predict. Run the
Y Spin Transform
display.
|
|
Having studied spin terms one at a time, we will now look at the
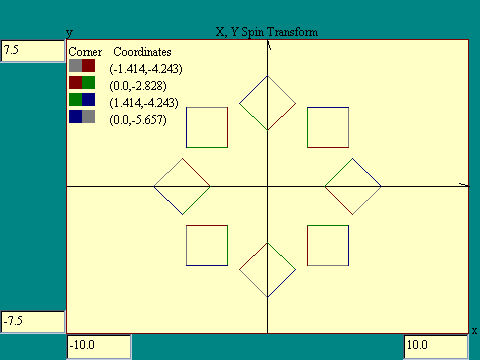
case where we have equal xspin and yspin in a transform. Run the
X,Y Spin Transform display.
|
|
|
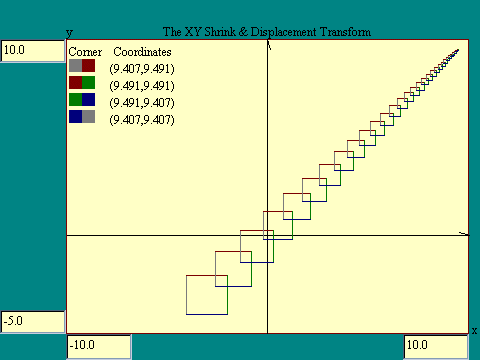
Now that we have examined displacement, sizing and spins
independently we will begin combining them. First a displacement
together with a size reduction. We will not concern ourselves
farther with size factors greater than 1 since these when
iterated cause points to diverge out of bounds, however large the
chosen limits. In this case the spin terms are zero and we shrink
the square in both dimensions while moving it in the +x and +y
direction. Notice that though the displacement remains fixed,
each successive iteration moves the square less distance. Run the
X,Y Shrink + X,Y Displacement Transforms
display.
|
|
As we saw in the last display, the combination of moving and
shrinking created a point on the display where all the points in
our square tended to end up under iteration. Such a focus is
referred to as a fixed point. We will see that any time we
iterate a transform where shrinkage in both dimensions is
invoked, we will find a fixed point somewhere. The location of
the fixed point will be determined by the interaction of all the
parameters. It is difficult to predict, just from the parameter
values where the fixed point will be because the effects are not
independent.
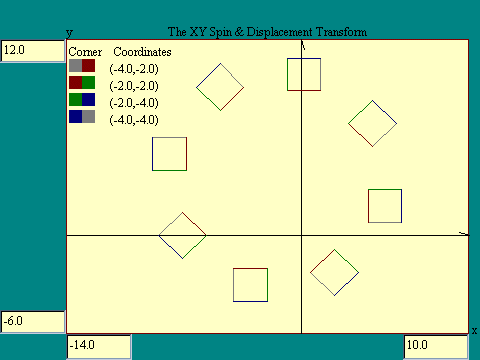
On the next display we will combine spin and displacement, this
time spinning counterclockwise by using positive values for xspin
and yspin. Try to visualize the effect you will get as you
iterate this transform. Run the
X,Y Spin + X,Y Displacement display.
|
|
|
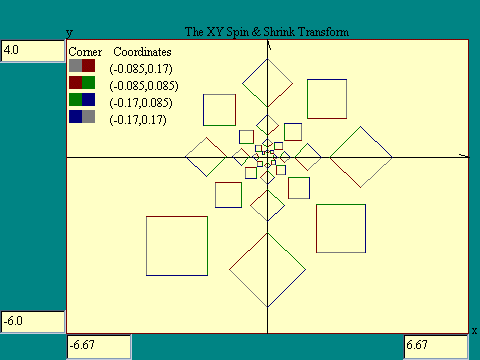
On the next display we drop the displacement and combine spin and
shrinking. Run the
X,Y Spin + X,Y Shrink Transform
display.
So far in this section of the program, we have worked with a
single transform which might incorporate shrink, spin and
displacement elements. In the next section we will examine the
effect of iterating multiple transforms.
Are there any questions?
|

 Next
Next
 Previous
Previous
 Other
Other
|




